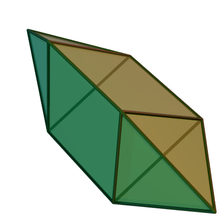
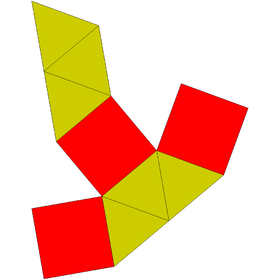
In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedra face-to-face. The same shape is also called the triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron and of a Johnson solid.
In geometry, the gyroelongated square bipyramid is a polyhedron with 16 triangular faces. it can be constructed from a square antiprism by attaching two equilateral square pyramids to each of its square faces. The same shape is also called hexakaidecadeltahedron, heccaidecadeltahedron, or tetrakis square antiprism; these last names mean a polyhedron with 16 triangular faces. It is an example of deltahedron, and of a Johnson solid.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In geometry, the pentagonal bipyramid is a polyhedron with 10 triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, and of Johnson solid.

In geometry, the gyroelongated square pyramid is the Johnson solid that can be constructed by attaching an equilateral square pyramid to a square antiprism. It occurs in chemistry; for example, the square antiprismatic molecular geometry.

In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. Many polyhedrons can be constructed involving the attachment of the base of a triangular cupola.

In geometry, the elongated triangular pyramid is one of the Johnson solids. As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically self-dual.

In geometry, the elongated square pyramid is a convex polyhedron constructed from a cube by attaching an equilateral square pyramid onto one of its faces. It is an example of Johnson solid. It is topologically self-dual.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

In geometry, the elongated pentagonal bipyramid is a polyhedron constructed by attaching two pentagonal pyramids onto the base of a pentagonal prism. It is an example of Johnson solid.
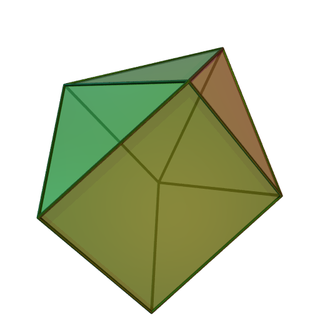
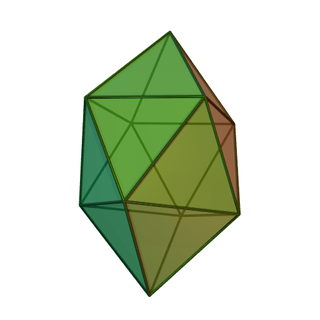
In geometry, the augmented triangular prism is a polyhedron constructed by attaching an equilateral square pyramid onto the square face of a triangular prism. As a result, it is an example of Johnson solid. It can be visualized as the chemical compound, known as capped trigonal prismatic molecular geometry.

In geometry, the biaugmented triangular prism is a polyhedron constructed from a triangular prism by attaching two equilateral square pyramids onto two of its square faces. It is an example of Johnson solid. It can be found in stereochemistry in bicapped trigonal prismatic molecular geometry.
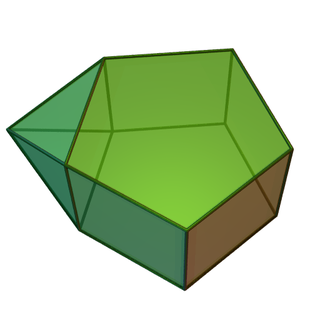
In geometry, the augmented pentagonal prism is a polyhedron that can be constructed by attaching an equilateral square pyramid onto the square face of pentagonal prism. It is an example of Johnson solid.

In geometry, the biaugmented pentagonal prism is a polyhedron constructed from a pentagonal prism by attaching two equilateral square pyramids onto each of its square faces. It is an example of Johnson solid.

In geometry, the augmented hexagonal prism is one of the Johnson solids. As the name suggests, it can be constructed by augmenting a hexagonal prism by attaching a square pyramid to one of its equatorial faces. When two or three such pyramids are attached, the result may be a parabiaugmented hexagonal prism, a metabiaugmented hexagonal prism, or a triaugmented hexagonal prism.

In geometry, the elongated triangular cupola is a polyhedron constructed from a hexagonal prism by attaching a triangular cupola. It is an example of a Johnson solid.

In geometry, the elongated triangular orthobicupola is a polyhedron constructed by attaching two regular triangular cupola into the base of a regular hexagonal prism. It is an example of Johnson solid.
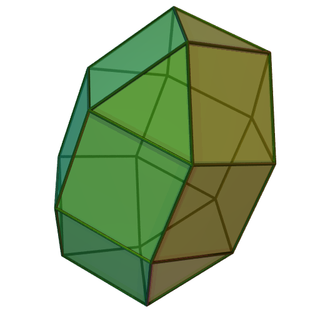
In geometry, the elongated triangular gyrobicupola is a polyhedron constructed by attaching two regular triangular cupolas to the base of a regular hexagonal prism, with one of them rotated in . It is an example of Johnson solid.

In geometry, the augmented truncated tetrahedron is a polyhedron constructed by attaching a triangular cupola onto an truncated tetrahedron. It is an example of a Johnson solid.

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.