Vector quantity

Last updated

In the natural sciences, a vector quantity (also known as a vector physical quantity, physical vector, or simply vector) is a vector-valued physical quantity. [1] [2] It is typically formulated as the product of a unit of measurement and a vector numerical value (unitless), often a Euclidean vector with magnitude and direction. For example, a position vector in physical space may be expressed as three Cartesian coordinates with SI unit of meters.

In physics and engineering, particularly in mechanics, a physical vector may be endowed with additional structure compared to a geometrical vector. [3] A bound vector is defined as the combination of an ordinary vector quantity and a point of application or point of action. [1] [4] Bound vector quantities are formulated as a directed line segment , with a definite initial point besides the magnitude and direction of the main vector. [1] [3] For example, a force on the Euclidean plane has two Cartesian components in SI unit of newtons and an accompanying two-dimensional position vector in meters, for a total of four numbers on the plane (and six in space). [5] [6] [4] A simpler example of a bound vector is the translation vector from an initial point to an end point; in this case, the bound vector is an ordered pair of points in the same position space, with all coordinates having the same quantity dimension and unit (length an meters). [7] [8] A sliding vector is the combination of an ordinary vector quantity and a line of application or line of action, over which the vector quantity can be translated (without rotations). A free vector is a vector quantity having an undefined support or region of application; it can be freely translated with no consequences; a displacement vector is a prototypical example of free vector.

Aside from the notion of units and support, physical vector quantities may also differ from Euclidean vectors in terms of metric. For example, an event in spacetime may be represented as a position four-vector, with coherent derived unit of meters: it includes a position Euclidean vector and a timelike component, t ⋅ c0 (involving the speed of light). In that case, the Minkowski metric is adopted instead of the Euclidean metric.

Vector quantities are a generalization of scalar quantities and can be further generalized as tensor quantities. [8] Individual vectors may be ordered in a sequence over time (a time series), such as position vectors discretizing a trajectory. A vector may also result from the evaluation, at a particular instant, of a continuous vector-valued function (e.g., the pendulum equation). In the natural sciences, the term "vector quantity" also encompasses vector fields defined over a two- or three-dimensional region of space, such as wind velocity over Earth's surface. Pseudo vectors and bivectors are also admitted as physical vector quantities.

See also

Related Research Articles

<span class="mw-page-title-main">Dimension</span> Property of a mathematical space

In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.

<span class="mw-page-title-main">Differential geometry</span> Branch of mathematics dealing with functions and geometric structures on differentiable manifolds

Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.

<span class="mw-page-title-main">Euclidean space</span> Fundamental space of geometry

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

<span class="mw-page-title-main">Euclidean vector</span> Geometric object that has length and direction

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Euclidean vectors can be added and scaled to form a vector space. A vector quantity is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a directed line segment. A vector is frequently depicted graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by

<span class="mw-page-title-main">Distance</span> Separation between two points

Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria. The term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects or a degree of separation. Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.

In physics and astronomy, a frame of reference is an abstract coordinate system, whose origin, orientation, and scale have been specified in physical space. It is based on a set of reference points, defined as geometric points whose position is identified both mathematically and physically . An important special case is that of inertial reference frames, a stationary or uniformly moving frame.

<span class="mw-page-title-main">Ball (mathematics)</span> Volume space bounded by a sphere

In mathematics, a ball is the solid figure bounded by a sphere; it is also called a solid sphere. It may be a closed ball or an open ball.

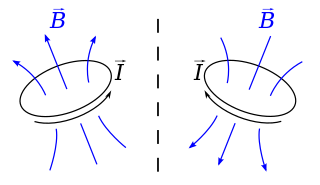
<span class="mw-page-title-main">Pseudovector</span> Physical quantity that changes sign with improper rotation

In physics and mathematics, a pseudovector is a quantity that behaves like a vector in many situations, but its direction does not conform when the object is rigidly transformed by rotation, translation, reflection, etc. This can also happen when the orientation of the space is changed. For example, the angular momentum is a pseudovector because it is often described as a vector, but by just changing the position of reference, angular momentum can reverse direction, which is not supposed to happen with true vectors.

<span class="mw-page-title-main">Minkowski space</span> Spacetime used in theory of relativity

In physics, Minkowski space is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.

A number line is a picture of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin point representing the number zero and evenly spaced marks in either direction representing integers, imagined to extend infinitely. The association between numbers and points on the line links arithmetical operations on numbers to geometric relations between points, and provides a conceptual framework for learning mathematics.

<span class="mw-page-title-main">Quotient</span> Mathematical result of division

In arithmetic, a quotient is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics. It has two definitions: either the integer part of a division or a fraction or ratio. For example, when dividing 20 by 3, the quotient is 6 in the first sense and in the second sense.

In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering of the class of objects to which it belongs. Magnitude as a concept dates to Ancient Greece and has been applied as a measure of distance from one object to another. For numbers, the absolute value of a number is commonly applied as the measure of units between a number and zero.

<span class="mw-page-title-main">Point (geometry)</span> Fundamental object of geometry

In geometry, a point is an abstract idealization of an exact position, without size, in physical space, or its generalization to other kinds of mathematical spaces. As zero-dimensional objects, points are usually taken to be the fundamental indivisible elements comprising the space, of which one-dimensional curves, two-dimensional surfaces, and higher-dimensional objects consist; conversely, a point can be determined by the intersection of two curves or three surfaces, called a vertex or corner.

<span class="mw-page-title-main">Orientation (vector space)</span> Choice of reference for distinguishing an object and its mirror image

The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented and which are "negatively" oriented. In the three-dimensional Euclidean space, right-handed bases are typically declared to be positively oriented, but the choice is arbitrary, as they may also be assigned a negative orientation. A vector space with an orientation selected is called an oriented vector space, while one not having an orientation selected, is called unoriented.

<span class="mw-page-title-main">Three-dimensional space</span> Geometric model of the physical space

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

Scalar quantities or simply scalars are physical quantities that can be described by a single pure number, accompanied by a unit of measurement, as in "10 cm" . Examples of scalar quantities are length, mass, charge, volume, and time. Scalars may represent the magnitude of physical quantities, such as speed is to velocity.

The mathematics of general relativity is complicated. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.

In mathematics and physics, vector is a term that refers to quantities that cannot be expressed by a single number, or to elements of some vector spaces. They have to be expressed by both magnitude and direction.

Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.

In geometry, an affine plane is a two-dimensional affine space.

References

  1. 1 2 3 "Details for IEV number 102-03-21: "vector quantity"". International Electrotechnical Vocabulary (in Japanese). Retrieved 2024-09-07.
  2. ↑ "Details for IEV number 102-03-04: "vector"". International Electrotechnical Vocabulary (in Japanese). Retrieved 2024-09-07.
  3. 1 2 Rao, A. (2006). Dynamics of Particles and Rigid Bodies: A Systematic Approach. Cambridge University Press. p. 3. ISBN   978-0-521-85811-3 . Retrieved 2024-09-08.
  4. 1 2 Teodorescu, Petre P. (2007-06-06). Mechanical Systems, Classical Models: Volume 1: Particle Mechanics. Springer Science & Business Media. ISBN   978-1-4020-5442-6.
  5. ↑ Merches, I.; Radu, D. (2014). Analytical Mechanics: Solutions to Problems in Classical Physics. CRC Press. p. 379. ISBN   978-1-4822-3940-9 . Retrieved 2024-09-09.
  6. ↑ Borisenko, A.I.; Tarapov, I.E.; Silverman, R.A. (2012). Vector and Tensor Analysis with Applications. Dover Books on Mathematics. Dover Publications. p. 2. ISBN   978-0-486-13190-0 . Retrieved 2024-09-08.
  7. ↑ "Appendix A. Linear Algebra from a Geometric Point of View". Differential Geometry: A Geometric Introduction. Ithaca, NY: David W. Henderson. 2013. pp. 121–138. doi:10.3792/euclid/9781429799843-13. ISBN   978-1-4297-9984-3.
  8. 1 2 "ISO 80000-2:2019 - Quantities and units - Part 2: Mathematics". ISO. 2013-08-20. Retrieved 2024-09-08.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.