 | This article needs additional citations for verification .(December 2022) |
Bean's critical state model, introduced by C. P. Bean [1] [2] in 1962, gives a macroscopic explanation of the irreversible magnetization behavior (hysteresis) of hard Type-II superconductors.
Hard superconductors often exhibit hysteresis in magnetization measurements. C. P. Bean postulated for the Shubnikov phase an extraordinary shielding process due to the microscopic structure of the materials. He assumed lossless transport with a critical current density Jc(B)(Jc(B→0) = const. and Jc(B→∞) = 0). An external magnetic field is shielded in the Meissner phase (H < Hc1) in the same way as in a soft superconductor. In the Shubnikov phase (Hc1 < H < Hc2), the critical current flows below the surface within a depth necessary to reduce the field in the inside of the superconductor to Hc1.
To understand the origin of the irreversible magnetization: assume a hollow cylinder in an external magnetic field parallel to the cylinder axis. [3] In the Meissner phase, a screening current is within the London penetration depth. Exceeding Hc1, vortices start to penetrate into the superconductor. These vortices are pinned on the surface (Bean–Livingston barrier). In the area below the surface, which is penetrated by the vortices, is a current with the density Jc. At low fields (H < H0), the vortices do not reach the inner surface of the hollow cylinder and the interior stays field-free. For H > H0, the vortices penetrate the whole cylinder and a magnetic field appears in the interior, which then increases with increasing external field. Let us now consider what happens, if the external field is then decreased: Due to induction, an opposed critical current is generated at the outer surface of the cylinder keeping inside the magnetic field for H0 < H < H1 constant. For H > H1, the opposed critical current penetrates the whole cylinder and the inner magnetic field starts to decrease with decreasing external field. When the external field vanishes, a remnant internal magnetic field occurs (comparable to the remanent magnetization of a ferromagnet). With an opposed external field H0, the internal magnetic field finally reaches 0T (H0 equates the coercive field of a ferromagnet).
Bean assumed a constant critical current meaning that H << Hc2. Kim et al. [4] extended the model assuming 1/J(H) proportional to H, yielding excellent agreement of theory and measurements on Nb3Sn tubes. Different geometries have to be considered as the irreversible magnetization depends on the sample geometry. [5]
Ferromagnetism is a property of certain materials that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are noticeably attracted to a magnet, which is a consequence of their substantial magnetic permeability.
Superconductivity is a set of physical properties observed in superconductors: materials where electrical resistance vanishes and magnetic fields are expelled from the material. Unlike an ordinary metallic conductor, whose resistance decreases gradually as its temperature is lowered, even down to near absolute zero, a superconductor has a characteristic critical temperature below which the resistance drops abruptly to zero. An electric current through a loop of superconducting wire can persist indefinitely with no power source.
A SQUID is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions.
In condensed-matter physics, the Meissner effect is the expulsion of a magnetic field from a superconductor during its transition to the superconducting state when it is cooled below the critical temperature. This expulsion will repel a nearby magnet.
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.
The magnetic flux, represented by the symbol Φ, threading some contour or loop is defined as the magnetic field B multiplied by the loop area S, i.e. Φ = B ⋅ S. Both B and S can be arbitrary, meaning that the flux Φ can be as well but increments of flux can be quantized. The wave function can be multivalued as it happens in the Aharonov–Bohm effect or quantized as in superconductors. The unit of quantization is therefore called magnetic flux quantum.
Magnesium diboride is the inorganic compound with the formula MgB2. It is a dark gray, water-insoluble solid. The compound has attracted attention because it becomes superconducting at 39 K (−234 °C). In terms of its composition, MgB2 differs strikingly from most low-temperature superconductors, which feature mainly transition metals. Its superconducting mechanism is primarily described by BCS theory.
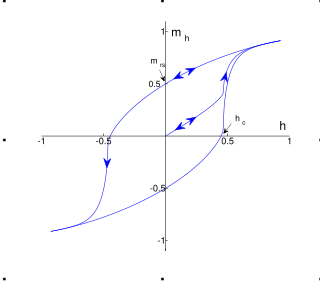
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.
Giant magnetoresistance (GMR) is a quantum mechanical magnetoresistance effect observed in multilayers composed of alternating ferromagnetic and non-magnetic conductive layers. The 2007 Nobel Prize in Physics was awarded to Albert Fert and Peter Grünberg for the discovery of GMR, which also sets the foundation for the study of spintronics.
Exchange bias or exchange anisotropy occurs in bilayers of magnetic materials where the hard magnetization behavior of an antiferromagnetic thin film causes a shift in the soft magnetization curve of a ferromagnetic film. The exchange bias phenomenon is of tremendous utility in magnetic recording, where it is used to pin the state of the readback heads of hard disk drives at exactly their point of maximum sensitivity; hence the term "bias."
In superconductivity, a type-II superconductor is a superconductor that exhibits an intermediate phase of mixed ordinary and superconducting properties at intermediate temperature and fields above the superconducting phases. It also features the formation of magnetic field vortices with an applied external magnetic field. This occurs above a certain critical field strength Hc1. The vortex density increases with increasing field strength. At a higher critical field Hc2, superconductivity is destroyed. Type-II superconductors do not exhibit a complete Meissner effect.
Lev Vasilyevich Shubnikov was a Soviet experimental physicist who worked in the Netherlands and USSR. He has been referred as the as 'the founding father of Soviet low-temperature physics'. He is known for the discovery of the Shubnikov–de Haas effect and type-II superconductivity. He also one of the first to discover antiferromagnetism.
In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases, quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.
A Josephson junction (JJ) is a quantum mechanical device which is made of two superconducting electrodes separated by a barrier. A π Josephson junction is a Josephson junction in which the Josephson phase φ equals π in the ground state, i.e. when no external current or magnetic field is applied.
In a standard superconductor, described by a complex field fermionic condensate wave function, vortices carry quantized magnetic fields because the condensate wave function is invariant to increments of the phase by . There a winding of the phase by creates a vortex which carries one flux quantum. See quantum vortex.
For a given temperature, the critical field refers to the maximum magnetic field strength below which a material remains superconducting. Superconductivity is characterized both by perfect conductivity and by the complete expulsion of magnetic fields. Changes in either temperature or magnetic flux density can cause the phase transition between normal and superconducting states. The highest temperature under which the superconducting state is seen is known as the critical temperature. At that temperature even the weakest external magnetic field will destroy the superconducting state, so the strength of the critical field is zero. As temperature decreases, the critical field increases generally to a maximum at absolute zero.
Flux pumping is a method for magnetising superconductors to fields in excess of 15 teslas. The method can be applied to any type II superconductor and exploits a fundamental property of superconductors, namely their ability to support and maintain currents on the length scale of the superconductor. Conventional magnetic materials are magnetised on a molecular scale which means that superconductors can maintain a flux density orders of magnitude bigger than conventional materials. Flux pumping is especially significant when one bears in mind that all other methods of magnetising superconductors require application of a magnetic flux density at least as high as the final required field. This is not true of flux pumping.
The demagnetizing field, also called the stray field, is the magnetic field (H-field) generated by the magnetization in a magnet. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement currents. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains in larger ferromagnets.
Macroscopic quantum phenomena are processes showing quantum behavior at the macroscopic scale, rather than at the atomic scale where quantum effects are prevalent. The best-known examples of macroscopic quantum phenomena are superfluidity and superconductivity; other examples include the quantum Hall effect, Josephson effect and topological order. Since 2000 there has been extensive experimental work on quantum gases, particularly Bose–Einstein condensates.