Superstripes

Last updated

Superstripes is a generic name for a phase with spatial broken symmetry that favors the onset of superconducting or superfluid quantum order. This scenario emerged in the 1990s when non-homogeneous metallic heterostructures at the atomic limit with a broken spatial symmetry have been found to favor superconductivity. [1] [2] Before a broken spatial symmetry was expected to compete and suppress the superconducting order. The driving mechanism for the amplification of the superconductivity critical temperature in superstripes matter has been proposed to be the shape resonance in the energy gap parameters ∆n that is a type of Fano resonance for coexisting condensates. [3] [4]

Contents

The superstripes show multigap superconductivity near a 2.5 Lifshitz transition where the renormalization of chemical potential at the metal-to-superconductor transition is not negligeable and the self-consistent solution of the gaps equation is required. The superstripes lattice scenario is made of puddles of multigap superstripes matter forming a superconducting network where different gaps are not only different in different portions of the k-space but also in different portions of the real space with a complex scale free distribution of Josephson junctions.

History

The term superstripes was introduced in 2000 at the international conference on "Stripes and High Tc Superconductivity" held in Rome to describe the particular phase of matter where a broken symmetry appearing at a transition from a phase with higher dimensionality N (3D or 2D) to a phase with lower dimensionality N-1 (2D or 1D) favors the superconducting or superfluid phase and it could increase the normal to superconducting transition temperature with the possible emergence of high-temperature superconductivity. The term superstripes scenario was introduced to make the key difference with the stripes scenario where the phase transition from a phase with higher dimensionality N (like a 2D electron gas) to the phase with broken symmetry and lower dimensionality (like a quasi 1D striped fluid) competes and suppresses the transition temperature to the superfluid phase and favors modulated striped magnetic ordering. In the broken symmetry of superstripes phase the structural modulation coexists and favors high-temperature superconductivity. [1]

Heterostructures at atomic limit

The prediction of high-temperature superconductivity transition temperatures is rightly considered to be one of the most difficult problems in theoretical physics. The problem remained elusive for many years since these materials have generally a very complex structure making unuseful theoretical modelling for a homogeneous system. The advances in experimental investigation on local lattice fluctuations have driven the community to the conclusion that it is a problem of quantum physics in complex matter. A growing paradigm for high-temperature superconductivity in superstripes is that a key term is the quantum interference effect between pairing channels, i.e., a resonance in the exchange-like, Josephson-like pair transfer term between different condensates. The quantum configuration interaction between different pairing channels is a particular case of shape resonance belonging to the group of Fano Feshbach resonances in atomic and nuclear physics. The critical temperature shows a suppression, due to a Fano antiresonance, when the chemical potential is tuned at a band edge where a new Fermi surface spot appears i.e., an "electronic topological transition" (ETT) or 2.5 Lifshitz transition or, a metal-to-metal topological transition. The Tc amplification is switched on when the chemical potential is tuned above the band edge in an energy region away from the band edge of the order of 1 or 2 times the energy cut off of the pairing interaction. The Tc is further amplified at the shape resonance if in this range the Fermi surface of the appearing fermi surface spot changes its dimensionality (for example the Lifshitz transition for opening a neck in a tubular Fermi surface). [5] The tuning of the chemical potential at the shape resonance can be obtained by changing: the charge density and/or the superlattice structural parameters, and/or the superlattice misfit strain and/or the disorder. Direct evidence for shape resonances in superstripes matter is provided by the anomalous variation of the isotope effect on the critical temperature by tuning the chemical potential. [6]

Materials

Crystal structure of the tetragonal (superconductive) phase of La2CuO4: top view (top-right) and CuO6 octahedron (bottom-right). La2CuO4 structure.png
Crystal structure of the tetragonal (superconductive) phase of La2CuO4: top view (top-right) and CuO6 octahedron (bottom-right).

It was known that the high-temperature cuprate superconductors have a complex lattice structure. [8] [9] [10] [11] [12] [13] [14] In 1993 it was proposed [15] that these materials belong to a particular class of materials called heterostructures at atomic limit made of a superlattice of superconducting atomic layers intercalated by a different material with the role of spacer.

All new high-temperature superconducting materials discovered in the years 2001–2013 are heterostructures at atomic limit made of the active atomic layers: honeycomb boron layer in diborides, graphene in intercalated graphite, CoO2 atomic bbc monolayers in cobaltates, FeAs atomic fluorite monolayers in pnictides, FeSe atomic fluorite monolayers in selenides.

In these materials the joint effect of (a) increasing the lattice misfit strain to a critical value, and (b) tuning the chemical potential near a Lifshitz transition in presence of electron-electron interactions induce a lattice instability with formation of the network of superconducting striped puddles in an insulating or metallic background.

This complex scenario has been called "superstripes scenario" where the 2D atomic layers show functional lattice inhomogeneities: "ripples puddles" of local lattice distortion have been observed in La2CuO4+y [16] [17] in Bi222; striped puddles of ordered dopants in the spacer layers have been seen in superoxygenated La2CuO4 [18] and in YBaCuO [19] The network of superconducting striped puddles has been found also in MFeAs pnictides [20] and recently in KFeSe selenides [21]

Self-organization of lattice defects can be controlled by strain engineering. [22] and photoinduced effects. [23]

Bose–Einstein condensates

Dispersion relations of a spin-orbit coupled system for different coupling strengths. Box A has no coupling. The dispersion relation shows 2 shifted free space dispersion relations. Box B shows how the gap at k=0 opens for weak coupling. Box C shows the strong coupling limit where the double degenerate minima in the first band merge into a single ground state at k=0. Spin orbit coupling dispersion relation.pdf
Dispersion relations of a spin–orbit coupled system for different coupling strengths. Box A has no coupling. The dispersion relation shows 2 shifted free space dispersion relations. Box B shows how the gap at k=0 opens for weak coupling. Box C shows the strong coupling limit where the double degenerate minima in the first band merge into a single ground state at k=0.

Superstripes (also called stripe phase) can also form in Bose–Einstein condensates (BEC) with spin–orbit coupling. The spin–orbit coupling is achieved by selecting 2 spin states from the manifold of hyperfine states to couple with a two photon process. [24] For weak coupling, the resulting Hamiltonian has a spectrum with a double degenerate ground state in the first band. In this regime, the single particle dispersion relation can host a BEC in each minima. [25] The result is that the BEC has 2 momentum components which can interfere in real space. The interference pattern will appear as fringes in the density of the BEC. The periodicity of the fringes is a result of the Raman coupling beam wavelength modified by the coupling strength and by interactions within the BEC. [25] Spin orbit coupling breaks the gauge symmetry of the system and the time reversal symmetry. The formation of the stripes breaks a continuous translational symmetry.

Recent efforts have attempted to observe the stripe phase in a Rubidium-87 BEC, however the stripes were too small and too low contrast to be detected. [24]

In 2017, two research groups from ETH Zurich and from MIT reported on the first creation of a supersolid with ultracold quantum gases. The MIT group exposed a Bose-Einstein condensate in a double-well potential to light beams that created an effective spin-orbit coupling. The interference between the atoms on the two spin-orbit coupled lattice sites gave rise to a density modulation that establishes a stripe phase with supersolid properties. [26] [27]

Related Research Articles

<span class="mw-page-title-main">BCS theory</span> Microscopic theory of superconductivity

In physics, theBardeen–Cooper–Schrieffer (BCS) theory is the first microscopic theory of superconductivity since Heike Kamerlingh Onnes's 1911 discovery. The theory describes superconductivity as a microscopic effect caused by a condensation of Cooper pairs. The theory is also used in nuclear physics to describe the pairing interaction between nucleons in an atomic nucleus.

<span class="mw-page-title-main">Condensed matter physics</span> Branch of physics

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models and predict the properties of extremely large groups of atoms.

<span class="mw-page-title-main">Superconductivity</span> Electrical conductivity with exactly zero resistance

Superconductivity is a set of physical properties observed in certain materials where electrical resistance vanishes and magnetic fields are expelled from the material. Any material exhibiting these properties is a superconductor. Unlike an ordinary metallic conductor, whose resistance decreases gradually as its temperature is lowered, even down to near absolute zero, a superconductor has a characteristic critical temperature below which the resistance drops abruptly to zero. An electric current through a loop of superconducting wire can persist indefinitely with no power source.

Unconventional superconductors are materials that display superconductivity which does not conform to conventional BCS theory or its extensions.

<span class="mw-page-title-main">High-temperature superconductivity</span> Superconductive behavior at temperatures much higher than absolute zero

High-temperature superconductors are defined as materials with critical temperature above 77 K, the boiling point of liquid nitrogen. They are only "high-temperature" relative to previously known superconductors, which function at even colder temperatures, close to absolute zero. The "high temperatures" are still far below ambient, and therefore require cooling. The first break through of high-temperature superconductor was discovered in 1986 by IBM researchers Georg Bednorz and K. Alex Müller. Although the critical temperature is around 35.1 K, this new type of superconductor was readily modified by Ching-Wu Chu to make the first high-temperature superconductor with critical temperature 93 K. Bednorz and Müller were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-Tc materials are type-II superconductors.

<span class="mw-page-title-main">Fermionic condensate</span> State of matter

A fermionic condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar conditions. The earliest recognized fermionic condensate described the state of electrons in a superconductor; the physics of other examples including recent work with fermionic atoms is analogous. The first atomic fermionic condensate was created by a team led by Deborah S. Jin using potassium-40 atoms at the University of Colorado Boulder in 2003.

The QCD vacuum is the quantum vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter.

A shape resonance is a metastable state in which an electron is trapped due to the shape of a potential barrier. Altunata describes a state as being a shape resonance if, "the internal state of the system remains unchanged upon disintegration of the quasi-bound level." A more general discussion of resonances and their taxonomies in molecular system can be found in the review article by Schulz,; for the discovery of the Fano resonance line-shape and for the Majorana pioneering work in this field by Antonio Bianconi; and for a mathematical review by Combes et al.

Color superconductivity is a phenomenon where matter carries color charge without loss, on analogy to the way conventional superconductors can carry electric charge without loss. Color superconductivity is predicted to occur in quark matter if the baryon density is sufficiently high (i.e., well above the density and energies of an atomic nucleus) and the temperature is not too high (well below 1012 kelvins). Color superconducting phases are to be contrasted with the normal phase of quark matter, which is just a weakly interacting Fermi liquid of quarks.

<span class="mw-page-title-main">Pseudogap</span> State at which a Fermi surface has a partial energy gap in condensed matter physics

In condensed matter physics, a pseudogap describes a state where the Fermi surface of a material possesses a partial energy gap, for example, a band structure state where the Fermi surface is gapped only at certain points.

A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.

Cuprate superconductors are a family of high-temperature superconducting materials made of layers of copper oxides (CuO2) alternating with layers of other metal oxides, which act as charge reservoirs. At ambient pressure, cuprate superconductors are the highest temperature superconductors known. However, the mechanism by which superconductivity occurs is still not understood.

Charge ordering (CO) is a phase transition occurring mostly in strongly correlated materials such as transition metal oxides or organic conductors. Due to the strong interaction between electrons, charges are localized on different sites leading to a disproportionation and an ordered superlattice. It appears in different patterns ranging from vertical to horizontal stripes to a checkerboard–like pattern , and it is not limited to the two-dimensional case. The charge order transition is accompanied by symmetry breaking and may lead to ferroelectricity. It is often found in close proximity to superconductivity and colossal magnetoresistance.

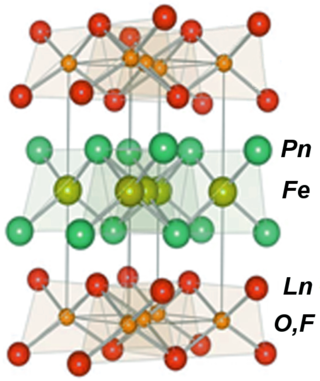
<span class="mw-page-title-main">Iron-based superconductor</span>

Iron-based superconductors (FeSC) are iron-containing chemical compounds whose superconducting properties were discovered in 2006. In 2008, led by recently discovered iron pnictide compounds, they were in the first stages of experimentation and implementation..

Type-1.5 superconductors are multicomponent superconductors characterized by two or more coherence lengths, at least one of which is shorter than the magnetic field penetration length , and at least one of which is longer. This is in contrast to single-component superconductors, where there is only one coherence length and the superconductor is necessarily either type 1 or type 2. When placed in magnetic field, type-1.5 superconductors should form quantum vortices: magnetic-flux-carrying excitations. They allow magnetic field to pass through superconductors due to a vortex-like circulation of superconducting particles. In type-1.5 superconductors these vortices have long-range attractive, short-range repulsive interaction. As a consequence a type-1.5 superconductor in a magnetic field can form a phase separation into domains with expelled magnetic field and clusters of quantum vortices which are bound together by attractive intervortex forces. The domains of the Meissner state retain the two-component superconductivity, while in the vortex clusters one of the superconducting components is suppressed. Thus such materials should allow coexistence of various properties of type-I and type-II superconductors.

<span class="mw-page-title-main">122 iron arsenide</span>

The 122 iron arsenide unconventional superconductors are part of a new class of iron-based superconductors. They form in the tetragonal I4/mmm, ThCr2Si2 type, crystal structure. The shorthand name "122" comes from their stoichiometry; the 122s have the chemical formula AEFe2Pn2, where AE stands for alkaline earth metal (Ca, Ba Sr or Eu) and Pn is pnictide (As, P, etc.). These materials become superconducting under pressure and also upon doping. The maximum superconducting transition temperature found to date is 38 K in the Ba0.6K0.4Fe2As2. The microscopic description of superconductivity in the 122s is yet unclear.

<span class="mw-page-title-main">Subir Sachdev</span> Indian physicist

Subir Sachdev is Herchel Smith Professor of Physics at Harvard University specializing in condensed matter. He was elected to the U.S. National Academy of Sciences in 2014, and received the Lars Onsager Prize from the American Physical Society and the Dirac Medal from the ICTP in 2018. He was a co-editor of the Annual Review of Condensed Matter Physics from 2017–2019.

<span class="mw-page-title-main">Distrontium ruthenate</span> Chemical compound

Distrontium ruthenate, also known as strontium ruthenate, is an oxide of strontium and ruthenium with the chemical formula Sr2RuO4. It was the first reported perovskite superconductor that did not contain copper. Strontium ruthenate is structurally very similar to the high-temperature cuprate superconductors, and in particular, is almost identical to the lanthanum doped superconductor (La, Sr)2CuO4. However, the transition temperature for the superconducting phase transition is 0.93 K (about 1.5 K for the best sample), which is much lower than the corresponding value for cuprates.

<span class="mw-page-title-main">Superfluidity</span> Fluid which flows without losing kinetic energy

Superfluidity is the characteristic property of a fluid with zero viscosity which therefore flows without any loss of kinetic energy. When stirred, a superfluid forms vortices that continue to rotate indefinitely. Superfluidity occurs in two isotopes of helium when they are liquefied by cooling to cryogenic temperatures. It is also a property of various other exotic states of matter theorized to exist in astrophysics, high-energy physics, and theories of quantum gravity. The theory of superfluidity was developed by Soviet theoretical physicists Lev Landau and Isaak Khalatnikov.

Elbio Rubén Dagotto is an Argentinian-American theoretical physicist and academic. He is a distinguished professor in the department of physics and astronomy at the University of Tennessee, Knoxville, and Distinguished Scientist in the Materials Science and Technology Division at the Oak Ridge National Laboratory.

References

  1. 1 2 Bianconi, A. (2000). "Superstripes". International Journal of Modern Physics B. 14 (29n31): 3289–3297. Bibcode:2000IJMPB..14.3289B. doi:10.1142/S0217979200003769.
  2. ↑ Bianconi, A.; Di Castro, D.; Saini, N. L.; Bianconi, G. (2002). "Superstripes". Phase Transitions and Self-Organization in Electronic and Molecular Networks. Fundamental Materials Research. p. 375. arXiv: 1107.4858 . doi:10.1007/0-306-47113-2_24. ISBN   978-0-306-46568-0. S2CID   118809015.
  3. ↑ Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N. L. (1996). "The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high TC". Solid State Communications. 100 (3): 181–186. arXiv: 1107.3292 . Bibcode:1996SSCom.100..181P. doi:10.1016/0038-1098(96)00373-0. S2CID   95957312.
  4. ↑ Bianconi, A.; Valletta, A.; Perali, A.; Saini, N. L. (1998). "Superconductivity of a striped phase at the atomic limit". Physica C: Superconductivity. 296 (3–4): 269. Bibcode:1998PhyC..296..269B. doi:10.1016/S0921-4534(97)01825-X.
  5. ↑ Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. (2010). "Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge". Physical Review B. 82 (18): 184528. arXiv: 1007.0510 . Bibcode:2010PhRvB..82r4528I. doi:10.1103/physrevb.82.184528. S2CID   119232655.
  6. ↑ Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. (2012). "Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes". Superconductor Science and Technology. 25 (12): 124002. arXiv: 1209.1528 . Bibcode:2012SuScT..25l4002P. doi:10.1088/0953-2048/25/12/124002. S2CID   118510526.
  7. ↑ Hosono, H.; Tanabe, K.; Takayama-Muromachi, E.; Kageyama, H.; Yamanaka, S.; Kumakura, H.; Nohara, M.; Hiramatsu, H.; Fujitsu, S. (2015). "Exploration of new superconductors and functional materials, and fabrication of superconducting tapes and wires of iron pnictides". Science and Technology of Advanced Materials. 16 (3): 033503. arXiv: 1505.02240 . Bibcode:2015STAdM..16c3503H. doi:10.1088/1468-6996/16/3/033503. PMC   5099821 . PMID   27877784.
  8. ↑ Müller, K. A. (2002). "From Phase Separation to Stripes". Stripes and Related Phenomena. Selected Topics in Superconductivity. Vol. 8. pp. 1–8. doi:10.1007/0-306-47100-0_1. ISBN   0-306-46419-5.
  9. ↑ Müller, K. A. (2005). "Essential Heterogeneities in Hole-Doped Cuprate Superconductors". Superconductivity in Complex Systems Structure and Bonding. Vol. 114. Berlin/Heidelberg: Springer. pp. 1–11. doi:10.1007/b101015. ISBN   978-3-540-31499-8.
  10. ↑ Raveau, B. (2007). "The perovskite history: More than 60 years of research from the discovery of ferroelectricity to colossal magnetoresistance via high TC superconductivity". Progress in Solid State Chemistry. 35 (2–4): 171–173. doi:10.1016/j.progsolidstchem.2007.04.001.
  11. ↑ Bishop, A. R. (2008). "HTC oxides: A collusion of spin, charge and lattice". Journal of Physics: Conference Series. 108 (1): 012027. Bibcode:2008JPhCS.108a2027B. doi: 10.1088/1742-6596/108/1/012027 .
  12. ↑ Bianconi, A (2000). Stripes and related phenomena. New York: Kluwer Academic/Plenum Publishers. ISBN   0-306-46419-5.
  13. ↑ Bianconi, A (2006). Symmetry and heterogeneity in high temperature superconductors. Dordrecht Great Britain: Springer. ISBN   9781402039881.
  14. ↑ Müller, K. A. (2005). Superconductivity in complex systems. Berlin New York: Springer. ISBN   978-3-540-23124-0.
  15. ↑ Bianconi, A. (1994). "On the possibility of new high Tc superconductors by producing metal heterostructures as in the cuprate perovskites". Solid State Communications. 89 (11): 933–936. arXiv: 1107.3249 . Bibcode:1994SSCom..89..933B. doi:10.1016/0038-1098(94)90354-9. S2CID   119243248.
  16. ↑ Di Castro, D.; Colapietro, M.; Bianconi, G. (2000). "Metallic stripes in oxygen doped La2CuO4" (PDF). International Journal of Modern Physics B. 14 (29n31): 3438. Bibcode:2000IJMPB..14.3438D. doi:10.1142/S0217979200003927.
  17. ↑ Poccia, N.; Ricci, A.; Campi, G.; Fratini, M.; Puri, A.; Gioacchino, D. D.; Marcelli, A.; Reynolds, M.; Burghammer, M.; Saini, N. L.; Aeppli, G.; Bianconi, A. (2012). "Optimum inhomogeneity of local lattice distortions in La2CuO4+y". Proceedings of the National Academy of Sciences. 109 (39): 15685–15690. arXiv: 1208.0101 . Bibcode:2012PNAS..10915685P. doi: 10.1073/pnas.1208492109 . PMC   3465392 . PMID   22961255.
  18. ↑ Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. (2010). "Scale-free structural organization of oxygen interstitials in La2CuO4+y". Nature. 466 (7308): 841–4. arXiv: 1008.2015 . Bibcode:2010Natur.466..841F. doi:10.1038/nature09260. PMID   20703301. S2CID   4405620.
  19. ↑ Campi, G.; Ricci, A.; Poccia, N.; Barba, L.; Arrighetti, G.; Burghammer, M.; Caporale, A. S.; Bianconi, A. (2013). "Scanning micro-x-ray diffraction unveils the distribution of oxygen chain nanoscale puddles in YBa2Cu3O6.33". Physical Review B. 87 (1): 014517. arXiv: 1212.2742 . Bibcode:2013PhRvB..87a4517C. doi:10.1103/physrevb.87.014517. S2CID   119233632.
  20. ↑ Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z. A.; Dong, X. L.; Yang, J.; Lu, W.; Zhao, Z. X.; Barba, L.; Bianconi, A. (2009). "Feshbach resonance and mesoscopic phase separation near a quantum critical point in multiband Fe As-based superconductors". Superconductor Science and Technology. 22 (1): 014004. arXiv: 0809.4865 . Bibcode:2009SuScT..22a4004C. doi:10.1088/0953-2048/22/1/014004. S2CID   55675041.
  21. ↑ Ricci, A.; Poccia, N.; Campi, G.; Joseph, B.; Arrighetti, G.; Barba, L.; Reynolds, M.; Burghammer, M.; Takeya, H.; Mizuguchi, Y.; Takano, Y.; Colapietro, M.; Saini, N. L.; Bianconi, A. (2011). "Nanoscale phase separation in the iron chalcogenide superconductor K0.8Fe1.6Se2 as seen via scanning nanofocused x-ray diffraction". Physical Review B. 84 (6): 060511. arXiv: 1107.0412 . Bibcode:2011PhRvB..84f0511R. doi:10.1103/physrevb.84.060511. S2CID   118364960.
  22. ↑ Agrestini, S.; Saini, N. L.; Bianconi, G.; Bianconi, A. (2003). "The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites". Journal of Physics A: Mathematical and General. 36 (35): 9133. Bibcode:2003JPhA...36.9133A. doi:10.1088/0305-4470/36/35/302.
  23. ↑ Poccia, N.; Fratini, M.; Ricci, A.; Campi, G.; Barba, L.; Vittorini-Orgeas, A.; Bianconi, G.; Aeppli, G.; Bianconi, A. (2011). "Evolution and control of oxygen order in a cuprate superconductor". Nature Materials. 10 (10): 733–6. arXiv: 1108.4120 . Bibcode:2011NatMa..10..733P. doi:10.1038/nmat3088. PMID   21857676. S2CID   40563268.
  24. 1 2 Galitski, Victor; Spielman, Ian B. (2013-02-07). "Spin-orbit coupling in quantum gases". Nature. 494 (7435): 49–54. arXiv: 1312.3292 . Bibcode:2013Natur.494...49G. doi:10.1038/nature11841. PMID   23389539. S2CID   240743.
  25. 1 2 Li, Yun; Pitaevskii, Lev P.; Stringari, Sandro (2012). "Quantum Tricriticality and Phase Transitions in Spin-Orbit Coupled Bose-Einstein Condensates". Physical Review Letters. 108 (22): 225301. arXiv: 1202.3036 . Bibcode:2012PhRvL.108v5301L. doi:10.1103/physrevlett.108.225301. PMID   23003610. S2CID   15680596.
  26. ↑ "MIT researchers create new form of matter". news.mit.edu. 2 March 2017. Retrieved 6 March 2017.
  27. ↑ Li, Jun-Ru; Lee, Jeongwon; Huang, Wujie; Burchesky, Sean; Shteynas, Boris; Top, Furkan Çağrı; Jamison, Alan O.; Ketterle, Wolfgang (1 March 2017). "A stripe phase with supersolid properties in spin–orbit-coupled Bose–Einstein condensates". Nature. 543 (7643): 91–94. arXiv: 1610.08194 . Bibcode:2017Natur.543...91L. doi:10.1038/nature21431. PMID   28252062. S2CID   4463520.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.