
In economics, profit maximization is the short run or long run process by which a firm may determine the price, input and output levels that will lead to the highest possible total profit. In neoclassical economics, which is currently the mainstream approach to microeconomics, the firm is assumed to be a "rational agent" which wants to maximize its total profit, which is the difference between its total revenue and its total cost.
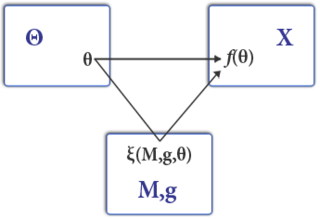
Mechanism design, sometimes called implementation theory or institutiondesign, is a branch of economics, social choice, and game theory that deals with designing game forms to implement a given social choice function. Because it starts with the end of the game and then works backwards to find a game that implements it, it is sometimes described as reverse game theory.

A Vickrey auction or sealed-bid second-price auction (SBSPA) is a type of sealed-bid auction. Bidders submit written bids without knowing the bid of the other people in the auction. The highest bidder wins but the price paid is the second-highest bid. This type of auction is strategically similar to an English auction and gives bidders an incentive to bid their true value. The auction was first described academically by Columbia University professor William Vickrey in 1961 though it had been used by stamp collectors since 1893. In 1797 Johann Wolfgang von Goethe sold a manuscript using a sealed-bid, second-price auction.
There are two fundamental theorems of welfare economics. The first states that in economic equilibrium, a set of complete markets, with complete information, and in perfect competition, will be Pareto optimal. The requirements for perfect competition are these:
- There are no externalities and each actor has perfect information.
- Firms and consumers take prices as given.

A shadow price is the monetary value assigned to an abstract or intangible commodity which is not traded in the marketplace. This often takes the form of an externality. Shadow prices are also known as the recalculation of known market prices in order to account for the presence of distortionary market instruments. Shadow prices are the real economic prices given to goods and services after they have been appropriately adjusted by removing distortionary market instruments and incorporating the societal impact of the respective good or service. A shadow price is often calculated based on a group of assumptions and estimates because it lacks reliable data, so it is subjective and somewhat inaccurate.
In mathematics and economics, the envelope theorem is a major result about the differentiability properties of the value function of a parameterized optimization problem. As we change parameters of the objective, the envelope theorem shows that, in a certain sense, changes in the optimizer of the objective do not contribute to the change in the objective function. The envelope theorem is an important tool for comparative statics of optimization models.
Competitive equilibrium is a concept of economic equilibrium, introduced by Kenneth Arrow and Gérard Debreu in 1951, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated.
The dual of a given linear program (LP) is another LP that is derived from the original LP in the following schematic way:

A Vickrey–Clarke–Groves (VCG) auction is a type of sealed-bid auction of multiple items. Bidders submit bids that report their valuations for the items, without knowing the bids of the other bidders. The auction system assigns the items in a socially optimal manner: it charges each individual the harm they cause to other bidders. It gives bidders an incentive to bid their true valuations, by ensuring that the optimal strategy for each bidder is to bid their true valuations of the items; it can be undermined by bidder collusion and in particular in some circumstances by a single bidder making multiple bids under different names. It is a generalization of a Vickrey auction for multiple items.
Monotone comparative statics is a sub-field of comparative statics that focuses on the conditions under which endogenous variables undergo monotone changes when there is a change in the exogenous parameters. Traditionally, comparative results in economics are obtained using the Implicit Function Theorem, an approach that requires the concavity and differentiability of the objective function as well as the interiority and uniqueness of the optimal solution. The methods of monotone comparative statics typically dispense with these assumptions. It focuses on the main property underpinning monotone comparative statics, which is a form of complementarity between the endogenous variable and exogenous parameter. Roughly speaking, a maximization problem displays complementarity if a higher value of the exogenous parameter increases the marginal return of the endogenous variable. This guarantees that the set of solutions to the optimization problem is increasing with respect to the exogenous parameter.
Fair item allocation is a kind of the fair division problem in which the items to divide are discrete rather than continuous. The items have to be divided among several partners who potentially value them differently, and each item has to be given as a whole to a single person. This situation arises in various real-life scenarios:
In mechanism design, a Vickrey–Clarke–Groves (VCG) mechanism is a generic truthful mechanism for achieving a socially optimal solution. It is a generalization of a Vickrey–Clarke–Groves auction. A VCG auction performs a specific task: dividing items among people. A VCG mechanism is more general: it can be used to select any outcome out of a set of possible outcomes.
A random-sampling mechanism (RSM) is a truthful mechanism that uses sampling in order to achieve approximately-optimal gain in prior-free mechanisms and prior-independent mechanisms.
A Bayesian-optimal mechanism (BOM) is a mechanism in which the designer does not know the valuations of the agents for whom the mechanism is designed, but the designer knows that they are random variables and knows the probability distribution of these variables.
A prior-free mechanism (PFM) is a mechanism in which the designer does not have any information on the agents' valuations, not even that they are random variables from some unknown probability distribution.
In mechanism design and auction theory, a profit extraction mechanism is a truthful mechanism whose goal is to win a pre-specified amount of profit, if it is possible.
A Prior-independent mechanism (PIM) is a mechanism in which the designer knows that the agents' valuations are drawn from some probability distribution, but does not know the distribution.
In auction theory, particularly Bayesian-optimal mechanism design, a virtual valuation of an agent is a function that measures the surplus that can be extracted from that agent.
Bayesian-optimal pricing is a kind of algorithmic pricing in which a seller determines the sell-prices based on probabilistic assumptions on the valuations of the buyers. It is a simple kind of a Bayesian-optimal mechanism, in which the price is determined in advance without collecting actual buyers' bids.
Regularity, sometimes called Myerson's regularity, is a property of probability distributions used in auction theory and revenue management. Examples of distributions that satisfy this condition include Gaussian, uniform, and exponential; some power law distributions also satisfy regularity. Distributions that satisfy the regularity condition are often referred to as "regular distributions".












