 | This article needs additional citations for verification .(December 2009) |
Flexural rigidity is defined as the force couple required to bend a fixed non-rigid structure by one unit of curvature, or as the resistance offered by a structure while undergoing bending.
Although the moment and displacement may vary along the length of the beam or rod, the flexural rigidity (defined as ) is a property of the beam itself and is generally constant. The flexural rigidity, moment, and transverse displacement are related by the following equation along the length of the rod, :
where is the flexural modulus (in Pa), is the second moment of area (in m4), is the transverse displacement of the beam at x, and is the bending moment at x. The flexural rigidity (stiffness) of the beam is therefore related to both , a material property, and , the physical geometry of the beam. If the material exhibits Isotropic behavior then the Flexural Modulus is equal to the Modulus of Elasticity (Young's Modulus).
Flexural rigidity has SI units of Pa·m4 (which also equals N·m²).
In the study of geology, lithospheric flexure affects the thin lithospheric plates covering the surface of the Earth when a load or force is applied to them. On a geological timescale, the lithosphere behaves elastically (in first approach) and can therefore bend under loading by mountain chains, volcanoes and other heavy objects. Isostatic depression caused by the weight of ice sheets during the last glacial period is an example of the effects of such loading.
The flexure of the plate depends on:
As flexural rigidity of the plate is determined by the Young's modulus, Poisson's ratio and cube of the plate's elastic thickness, it is a governing factor in both (1) and (2).
Flexural Rigidity [1]
= elastic thickness (~5–100 km)
Flexural rigidity of a plate has units of Pa·m3, i.e. one dimension of length less than the same property for the rod, as it refers to the moment per unit length per unit of curvature, and not the total moment. I is termed as moment of inertia. J is denoted as 2nd moment of inertia/polar moment of inertia.
Sedimentary basins are regions of the Earth where long-term subsidence creates accommodation space for accumulation of sediments. As the sediments are buried, they are subject to increasing pressure and begin the processes of compaction and lithification that transform them into sedimentary rock.
Isostasy or isostatic equilibrium is the state of gravitational equilibrium between Earth's crust and mantle such that the crust "floats" at an elevation that depends on its thickness and density. This concept is invoked to explain how different topographic heights can exist at Earth's surface. Although originally defined in terms of continental crust and mantle, it has subsequently been interpreted in terms of lithosphere and asthenosphere, particularly with respect to oceanic island volcanoes, such as the Hawaiian Islands.
Stiffness is the extent to which an object resists deformation in response to an applied force.
In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress in slender columns.
In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.
The outer trench swell, outer trench high, or outer rise is a subtle ridge on the seafloor near an oceanic trench, where a descending plate begins to flex and fault in preparation for its descent into the mantle at a subduction zone. The lithosphere is bent upwards by plate stresses, and is not in isostatic equilibrium.
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol .
The polar moment , also known as second (polar) moment of area, is a quantity used to describe resistance to torsional deformation (deflection), in cylindrical objects with an invariant cross-section and no significant warping or out-of-plane deformation. It is a constituent of the second moment of area, linked through the perpendicular axis theorem. Where the planar second moment of area describes an object's resistance to deflection (bending) when subjected to a force applied to a plane parallel to the central axis, the polar second moment of area describes an object's resistance to deflection when subjected to a moment applied in a plane perpendicular to the object's central axis. Similar to planar second moment of area calculations, the polar second moment of area is often denoted as . While several engineering textbooks and academic publications also denote it as or , this designation should be given careful attention so that it does not become confused with the torsion constant, , used for non-cylindrical objects.
Tonewood refers to specific wood varieties that possess tonal properties that make them good choices for use in woodwind or acoustic stringed instruments.
In mechanics, the flexural modulus or bending modulus is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test, and uses units of force per area. The flexural modulus defined using the 3-point bend test assumes a linear stress strain response.
The Timoshenko–Ehrenfest beam theory was developed by Stephen Timoshenko and Paul Ehrenfest early in the 20th century. The model takes into account shear deformation and rotational bending effects, making it suitable for describing the behaviour of thick beams, sandwich composite beams, or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam. The resulting equation is of 4th order but, unlike Euler–Bernoulli beam theory, there is also a second-order partial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.
Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include area for tension and shear, radius of gyration for compression, and moment of inertia and polar moment of inertia for stiffness. Any relationship between these properties is highly dependent on the shape in question. Equations for the section moduli of common shapes are given below. There are two types of section moduli, the elastic section modulus and the plastic section modulus. The section moduli of different profiles can also be found as numerical values for common profiles in tables listing properties of such.
In engineering, deflection is the degree to which a part of a structural element is displaced under a load. It may refer to an angle or a distance.
Structural engineering depends upon a detailed knowledge of loads, physics and materials to understand and predict how structures support and resist self-weight and imposed loads. To apply the knowledge successfully structural engineers will need a detailed knowledge of mathematics and of relevant empirical and theoretical design codes. They will also need to know about the corrosion resistance of the materials and structures, especially when those structures are exposed to the external environment.
In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions. The typical thickness to width ratio of a plate structure is less than 0.1. A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation and stresses in a plate subjected to loads.
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
Lithospheric flexure is the process by which the lithosphere bends under the action of forces such as the weight of a growing orogen or changes in ice thickness related to (de)glaciations. The lithosphere rests on the asthenosphere, a viscous layer that in geological time scales behaves like a fluid. Thus, when loaded, the lithosphere progressively reaches an isostatic equilibrium, which represents the Archimedes principle applied to geological settings.
The moment-area theorem is an engineering tool to derive the slope, rotation and deflection of beams and frames. This theorem was developed by Mohr and later stated namely by Charles Ezra Greene in 1873. This method is advantageous when we solve problems involving beams, especially for those subjected to a series of concentrated loadings or having segments with different moments of inertia.
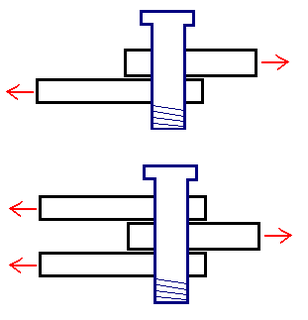
The four-point flexural test provides values for the modulus of elasticity in bending , flexural stress , flexural strain and the flexural stress-strain response of the material. This test is very similar to the three-point bending flexural test. The major difference being that with the addition of a fourth bearing the portion of the beam between the two loading points is put under maximum stress, as opposed to only the material right under the central bearing in the case of three point bending.
