
The kilogram is the base unit of mass in the International System of Units (SI), having the unit symbol kg. 'Kilogram' means 'one thousand grams' and is colloquially abbreviated to kilo.

The International System of Units, internationally known by the abbreviation SI, is the modern form of the metric system and the world's most widely used system of measurement. Coordinated by the International Bureau of Weights and Measures it is the only system of measurement with official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce.
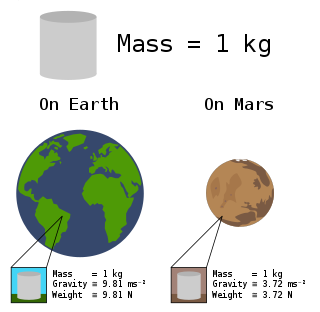
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.

The metric system is a decimal-based system of measurement. The current international standard for the metric system is the International System of Units, in which all units can be expressed in terms of seven base units: the metre (m), kilogram (kg), second (s), ampere (A), kelvin (K), mole (mol), and candela (cd). These can be made into larger or smaller units with the use of metric prefixes.

The pascal is the unit of pressure in the International System of Units (SI). It is also used to quantify internal pressure, stress, Young's modulus, and ultimate tensile strength. The unit, named after Blaise Pascal, is an SI coherent derived unit defined as one newton per square metre (N/m2). It is also equivalent to 10 barye in the CGS system. Common multiple units of the pascal are the hectopascal, which is equal to one millibar, and the kilopascal, which is equal to one centibar.

Physical geodesy is the study of the physical properties of Earth's gravity and its potential field, with a view to their application in geodesy.
The pound of force or pound-force is a unit of force used in some systems of measurement, including English Engineering units and the foot–pound–second system.

The newton-metre or newton-meter is the unit of torque in the International System of Units (SI). One newton-metre is equal to the torque resulting from a force of one newton applied perpendicularly to the end of a moment arm that is one metre long.
The kilogram-force, or kilopond, is a non-standard gravitational metric unit of force. It is not accepted for use with the International System of Units (SI) and is deprecated for most uses. The kilogram-force is equal to the magnitude of the force exerted on one kilogram of mass in a 9.80665 m/s2 gravitational field. That is, it is the weight of a kilogram under standard gravity. One kilogram-force is defined as 9.80665 N. Similarly, a gram-force is 9.80665 mN, and a milligram-force is 9.80665 μN.

The standard atmosphere is a unit of pressure defined as 101325 Pa. It is sometimes used as a reference pressure or standard pressure. It is approximately equal to Earth's average atmospheric pressure at sea level.
The metre per second squared is the unit of acceleration in the International System of Units (SI). As a derived unit, it is composed from the SI base units of length, the metre, and time, the second. Its symbol is written in several forms as m/s2, m·s−2 or ms−2, , or less commonly, as (m/s)/s.

The newton-second is the unit of impulse in the International System of Units (SI). It is dimensionally equivalent to the momentum unit kilogram-metre per second (kg⋅m/s). One newton-second corresponds to a one-newton force applied for one second.

A kilogram-force per square centimetre (kgf/cm2), often just kilogram per square centimetre (kg/cm2), or kilopond per square centimetre (kp/cm2) is a deprecated unit of pressure using metric units. It is not a part of the International System of Units (SI), the modern metric system. 1 kgf/cm2 equals 98.0665 kPa (kilopascals) or 0.980665 bar—2% less than a bar. It is also known as a technical atmosphere.
The gravitational metric system is a non-standard system of units, which does not comply with the International System of Units (SI). It is built on the three base quantities length, time and force with base units metre, second and kilopond respectively. Internationally used abbreviations of the system are MKpS, MKfS or MKS . However, the abbreviation MKS is also used for the MKS system of units, which, like the SI, uses mass in kilogram as a base unit.
The foot–pound–second system is a system of units built on three fundamental units: the foot for length, the (avoirdupois) pound for either mass or force, and the second for time.

The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force . It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm .

In common usage, the mass of an object is often referred to as its weight, though these are in fact different concepts and quantities. Nevertheless, one object will always weigh more than another with less mass if both are subject to the same gravity.

In 2019, four of the seven SI base units specified in the International System of Quantities were redefined in terms of natural physical constants, rather than human artefacts such as the standard kilogram. Effective 20 May 2019, the 144th anniversary of the Metre Convention, the kilogram, ampere, kelvin, and mole are now defined by setting exact numerical values, when expressed in SI units, for the Planck constant, the elementary electric charge, the Boltzmann constant, and the Avogadro constant, respectively. The second, metre, and candela had previously been redefined using physical constants. The four new definitions aimed to improve the SI without changing the value of any units, ensuring continuity with existing measurements. In November 2018, the 26th General Conference on Weights and Measures (CGPM) unanimously approved these changes, which the International Committee for Weights and Measures (CIPM) had proposed earlier that year after determining that previously agreed conditions for the change had been met. These conditions were satisfied by a series of experiments that measured the constants to high accuracy relative to the old SI definitions, and were the culmination of decades of research.

The history of the metric system began during the Age of Enlightenment with measures of length and weight derived from nature, along with their decimal multiples and fractions. The system became the standard of France and Europe within half a century. Other measures with unity ratios were added, and the system went on to be adopted across the world.
Since its introduction in 1960, the base units for the International system of units, known as SI, have changed several times. Tables in this article summarize those changes.




















