Plate theory

For the theory of geological plates, see Plate tectonics.

Vibration mode of a clamped square plate

In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draw on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions. ^[1] The typical thickness to width ratio of a plate structure is less than 0.1.^{[ citation needed ]} A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation and stresses in a plate subjected to loads.

Of the numerous plate theories that have been developed since the late 19th century, two are widely accepted and used in engineering. These are

• the Kirchhoff–Love theory of plates (classical plate theory)
• The Uflyand-Mindlin theory of plates (first-order shear plate theory)

Kirchhoff–Love theory for thin plates

Main article: Kirchhoff–Love plate theory

Note: the Einstein summation convention of summing on repeated indices is used below.

Deformation of a thin plate highlighting the displacement, the mid-surface (red) and the normal to the mid-surface (blue)

The Kirchhoff–Love theory is an extension of Euler–Bernoulli beam theory to thin plates. The theory was developed in 1888 by Love ^[2] using assumptions proposed by Kirchhoff. It is assumed that a mid-surface plane can be used to represent the three-dimensional plate in two-dimensional form.

The following kinematic assumptions are made in this theory: ^[3]

• straight lines normal to the mid-surface remain straight after deformation
• straight lines normal to the mid-surface remain normal to the mid-surface after deformation
• the thickness of the plate does not change during a deformation.

Displacement field

The Kirchhoff hypothesis implies that the displacement field has the form

${\displaystyle {\begin{aligned}u_{\alpha }(\mathbf {x} )&=u_{\alpha }^{0}(x_{1},x_{2})-x_{3}~{\frac {\partial w^{0}}{\partial x_{\alpha }}}=u_{\alpha }^{0}-x_{3}~w_{,\alpha }^{0}~;~~\alpha =1,2\\u_{3}(\mathbf {x} )&=w^{0}(x_{1},x_{2})\end{aligned}}}$

where ${\displaystyle x_{1}}$ and ${\displaystyle x_{2}}$ are the Cartesian coordinates on the mid-surface of the undeformed plate, ${\displaystyle x_{3}}$ is the coordinate for the thickness direction, ${\displaystyle u_{1}^{0},u_{2}^{0}}$ are the in-plane displacements of the mid-surface, and ${\displaystyle w^{0}}$ is the displacement of the mid-surface in the ${\displaystyle x_{3}}$ direction.

If ${\displaystyle \varphi _{\alpha }}$ are the angles of rotation of the normal to the mid-surface, then in the Kirchhoff–Love theory ${\displaystyle \varphi _{\alpha }=w_{,\alpha }^{0}\,.}$

Displacement of the mid-surface (left) and of a normal (right)

Strain-displacement relations

For the situation where the strains in the plate are infinitesimal and the rotations of the mid-surface normals are less than 10° the strains-displacement relations are

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\tfrac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}}$

Therefore, the only non-zero strains are in the in-plane directions.

If the rotations of the normals to the mid-surface are in the range of 10° to 15°, the strain-displacement relations can be approximated using the von Kármán strains. Then the kinematic assumptions of Kirchhoff-Love theory lead to the following strain-displacement relations

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0}+w_{,\alpha }^{0}~w_{,\beta }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}}$

This theory is nonlinear because of the quadratic terms in the strain-displacement relations.

Equilibrium equations

The equilibrium equations for the plate can be derived from the principle of virtual work. For the situation where the strains and rotations of the plate are small, the equilibrium equations for an unloaded plate are given by

${\displaystyle {\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }&=0\end{aligned}}}$

where the stress resultants and stress moment resultants are defined as

${\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}}$

and the thickness of the plate is ${\displaystyle 2h}$. The quantities ${\displaystyle \sigma _{\alpha \beta }}$ are the stresses.

If the plate is loaded by an external distributed load ${\displaystyle q(x)}$ that is normal to the mid-surface and directed in the positive ${\displaystyle x_{3}}$ direction, the principle of virtual work then leads to the equilibrium equations

${\displaystyle {\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }-q&=0\end{aligned}}}$

For moderate rotations, the strain-displacement relations take the von Karman form and the equilibrium equations can be expressed as

${\displaystyle {\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }+[N_{\alpha \beta }~w_{,\beta }^{0}]_{,\alpha }-q&=0\end{aligned}}}$

Boundary conditions

The boundary conditions that are needed to solve the equilibrium equations of plate theory can be obtained from the boundary terms in the principle of virtual work.

For small strains and small rotations, the boundary conditions are

${\displaystyle {\begin{aligned}n_{\alpha }~N_{\alpha \beta }&\quad \mathrm {or} \quad u_{\beta }^{0}\\n_{\alpha }~M_{\alpha \beta ,\beta }&\quad \mathrm {or} \quad w^{0}\\n_{\beta }~M_{\alpha \beta }&\quad \mathrm {or} \quad w_{,\alpha }^{0}\end{aligned}}}$

Note that the quantity ${\displaystyle n_{\alpha }~M_{\alpha \beta ,\beta }}$ is an effective shear force.

Stress–strain relations

The stress–strain relations for a linear elastic Kirchhoff plate are given by

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}}$

Since ${\displaystyle \sigma _{\alpha 3}}$ and ${\displaystyle \sigma _{33}}$ do not appear in the equilibrium equations it is implicitly assumed that these quantities do not have any effect on the momentum balance and are neglected.

It is more convenient to work with the stress and moment resultants that enter the equilibrium equations. These are related to the displacements by

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}=\left\{\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}}$

and

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-\left\{\int _{-h}^{h}x_{3}^{2}~{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}\,.}$

The extensional stiffnesses are the quantities

${\displaystyle A_{\alpha \beta }:=\int _{-h}^{h}C_{\alpha \beta }~dx_{3}}$

The bending stiffnesses (also called flexural rigidity) are the quantities

${\displaystyle D_{\alpha \beta }:=\int _{-h}^{h}x_{3}^{2}~C_{\alpha \beta }~dx_{3}}$

Isotropic and homogeneous Kirchhoff plate

Main article: Kirchhoff–Love plate theory

For an isotropic and homogeneous plate, the stress–strain relations are

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.}$

The moments corresponding to these stresses are

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}}$

Pure bending

The displacements ${\displaystyle u_{1}^{0}}$ and ${\displaystyle u_{2}^{0}}$ are zero under pure bending conditions. For an isotropic, homogeneous plate under pure bending the governing equation is

${\displaystyle {\frac {\partial ^{4}w}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w}{\partial x_{2}^{4}}}=0\quad {\text{where}}\quad w:=w^{0}\,.}$

In index notation,

${\displaystyle w_{,1111}^{0}+2~w_{,1212}^{0}+w_{,2222}^{0}=0\,.}$

In direct tensor notation, the governing equation is

${\displaystyle \nabla ^{2}\nabla ^{2}w=0\,.}$

Transverse loading

For a transversely loaded plate without axial deformations, the governing equation has the form

${\displaystyle {\frac {\partial ^{4}w}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w}{\partial x_{2}^{4}}}=-{\frac {q}{D}}}$

where

${\displaystyle D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.}$

for a plate with thickness ${\displaystyle 2h}$. In index notation,

${\displaystyle w_{,1111}^{0}+2\,w_{,1212}^{0}+w_{,2222}^{0}=-{\frac {q}{D}}}$

and in direct notation

${\displaystyle \nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}}\,.}$

In cylindrical coordinates ${\displaystyle (r,\theta ,z)}$, the governing equation is

${\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.}$

Orthotropic and homogeneous Kirchhoff plate

For an orthotropic plate

${\displaystyle {\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}={\cfrac {1}{1-\nu _{12}\nu _{21}}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}\,.}$

Therefore,

${\displaystyle {\begin{bmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{bmatrix}}={\cfrac {2h}{1-\nu _{12}\nu _{21}}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}}$

and

${\displaystyle {\begin{bmatrix}D_{11}&D_{12}&D_{13}\\D_{21}&D_{22}&D_{23}\\D_{31}&D_{32}&D_{33}\end{bmatrix}}={\cfrac {2h^{3}}{3(1-\nu _{12}\nu _{21})}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}\,.}$

Transverse loading

The governing equation of an orthotropic Kirchhoff plate loaded transversely by a distributed load ${\displaystyle q}$ per unit area is

${\displaystyle D_{x}w_{,1111}^{0}+2D_{xy}w_{,1122}^{0}+D_{y}w_{,2222}^{0}=-q}$

where

${\displaystyle {\begin{aligned}D_{x}&=D_{11}={\frac {2h^{3}E_{1}}{3(1-\nu _{12}\nu _{21})}}\\D_{y}&=D_{22}={\frac {2h^{3}E_{2}}{3(1-\nu _{12}\nu _{21})}}\\D_{xy}&=D_{33}+{\tfrac {1}{2}}(\nu _{21}D_{11}+\nu _{12}D_{22})=D_{33}+\nu _{21}D_{11}={\frac {4h^{3}G_{12}}{3}}+{\frac {2h^{3}\nu _{21}E_{1}}{3(1-\nu _{12}\nu _{21})}}\,.\end{aligned}}}$

Dynamics of thin Kirchhoff plates

Main article: Kirchhoff–Love plate theory

The dynamic theory of plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes.

Governing equations

The governing equations for the dynamics of a Kirchhoff–Love plate are

${\displaystyle {\begin{aligned}N_{\alpha \beta ,\beta }&=J_{1}~{\ddot {u}}_{\alpha }^{0}\\M_{\alpha \beta ,\alpha \beta }-q(x,t)&=J_{1}~{\ddot {w}}^{0}-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}\end{aligned}}}$

where, for a plate with density ${\displaystyle \rho =\rho (x)}$,

${\displaystyle J_{1}:=\int _{-h}^{h}\rho ~dx_{3}=2~\rho ~h~;~~J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}={\frac {2}{3}}~\rho ~h^{3}}$

and

${\displaystyle {\dot {u}}_{i}={\frac {\partial u_{i}}{\partial t}}~;~~{\ddot {u}}_{i}={\frac {\partial ^{2}u_{i}}{\partial t^{2}}}~;~~u_{i,\alpha }={\frac {\partial u_{i}}{\partial x_{\alpha }}}~;~~u_{i,\alpha \beta }={\frac {\partial ^{2}u_{i}}{\partial x_{\alpha }\partial x_{\beta }}}}$

The figures below show some vibrational modes of a circular plate.

• 
  mode k = 0, p = 1
• 
  mode k = 1, p = 2

Isotropic plates

The governing equations simplify considerably for isotropic and homogeneous plates for which the in-plane deformations can be neglected and have the form

${\displaystyle D\,\left({\frac {\partial ^{4}w^{0}}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w^{0}}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w^{0}}{\partial x_{2}^{4}}}\right)=-q(x_{1},x_{2},t)-2\rho h\,{\frac {\partial ^{2}w^{0}}{\partial t^{2}}}\,.}$

where ${\displaystyle D}$ is the bending stiffness of the plate. For a uniform plate of thickness ${\displaystyle 2h}$,

${\displaystyle D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.}$

In direct notation

${\displaystyle D\,\nabla ^{2}\nabla ^{2}w^{0}=-q(x,y,t)-2\rho h\,{\ddot {w}}^{0}\,.}$

Uflyand-Mindlin theory for thick plates

Main article: Mindlin–Reissner plate theory

Note: the Einstein summation convention of summing on repeated indices is used below.

In the theory of thick plates, or theory of Yakov S. Uflyand ^[4] (see, for details, Elishakoff's handbook ^[5] ), Raymond Mindlin ^[6] and Eric Reissner, the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. If ${\displaystyle \varphi _{1}}$ and ${\displaystyle \varphi _{2}}$ designate the angles which the mid-surface makes with the ${\displaystyle x_{3}}$ axis then

${\displaystyle \varphi _{1}\neq w_{,1}~;~~\varphi _{2}\neq w_{,2}}$

Then the Mindlin–Reissner hypothesis implies that

${\displaystyle {\begin{aligned}u_{\alpha }(\mathbf {x} )&=u_{\alpha }^{0}(x_{1},x_{2})-x_{3}~\varphi _{\alpha }~;~~\alpha =1,2\\u_{3}(\mathbf {x} )&=w^{0}(x_{1},x_{2})\end{aligned}}}$

Strain-displacement relations

Depending on the amount of rotation of the plate normals two different approximations for the strains can be derived from the basic kinematic assumptions.

For small strains and small rotations the strain-displacement relations for Mindlin–Reissner plates are

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0})-{\frac {x_{3}}{2}}~(\varphi _{\alpha ,\beta }+\varphi _{\beta ,\alpha })\\\varepsilon _{\alpha 3}&={\cfrac {1}{2}}\left(w_{,\alpha }^{0}-\varphi _{\alpha }\right)\\\varepsilon _{33}&=0\end{aligned}}}$

The shear strain, and hence the shear stress, across the thickness of the plate is not neglected in this theory. However, the shear strain is constant across the thickness of the plate. This cannot be accurate since the shear stress is known to be parabolic even for simple plate geometries. To account for the inaccuracy in the shear strain, a shear correction factor (${\displaystyle \kappa }$) is applied so that the correct amount of internal energy is predicted by the theory. Then

${\displaystyle \varepsilon _{\alpha 3}={\cfrac {1}{2}}~\kappa ~\left(w_{,\alpha }^{0}-\varphi _{\alpha }\right)}$

Equilibrium equations

The equilibrium equations have slightly different forms depending on the amount of bending expected in the plate. For the situation where the strains and rotations of the plate are small the equilibrium equations for a Mindlin–Reissner plate are

${\displaystyle {\begin{aligned}&N_{\alpha \beta ,\alpha }=0\\&M_{\alpha \beta ,\beta }-Q_{\alpha }=0\\&Q_{\alpha ,\alpha }+q=0\,.\end{aligned}}}$

The resultant shear forces in the above equations are defined as

${\displaystyle Q_{\alpha }:=\kappa ~\int _{-h}^{h}\sigma _{\alpha 3}~dx_{3}\,.}$

Boundary conditions

The boundary conditions are indicated by the boundary terms in the principle of virtual work.

If the only external force is a vertical force on the top surface of the plate, the boundary conditions are

${\displaystyle {\begin{aligned}n_{\alpha }~N_{\alpha \beta }&\quad \mathrm {or} \quad u_{\beta }^{0}\\n_{\alpha }~M_{\alpha \beta }&\quad \mathrm {or} \quad \varphi _{\alpha }\\n_{\alpha }~Q_{\alpha }&\quad \mathrm {or} \quad w^{0}\end{aligned}}}$

Constitutive relations

The stress–strain relations for a linear elastic Mindlin–Reissner plate are given by

${\displaystyle {\begin{aligned}\sigma _{\alpha \beta }&=C_{\alpha \beta \gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{\alpha 3}&=C_{\alpha 3\gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{33}&=C_{33\gamma \theta }~\varepsilon _{\gamma \theta }\end{aligned}}}$

Since ${\displaystyle \sigma _{33}}$ does not appear in the equilibrium equations it is implicitly assumed that it do not have any effect on the momentum balance and is neglected. This assumption is also called the plane stress assumption. The remaining stress–strain relations for an orthotropic material, in matrix form, can be written as

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{23}\\\sigma _{31}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&0&0&0\\C_{12}&C_{22}&0&0&0\\0&0&C_{44}&0&0\\0&0&0&C_{55}&0\\0&0&0&0&C_{66}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{23}\\\varepsilon _{31}\\\varepsilon _{12}\end{bmatrix}}}$

Then,

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}=\left\{\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&0\\C_{12}&C_{22}&0\\0&0&C_{66}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}}$

and

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-\left\{\int _{-h}^{h}x_{3}^{2}~{\begin{bmatrix}C_{11}&C_{12}&0\\C_{12}&C_{22}&0\\0&0&C_{66}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}\varphi _{1,1}\\\varphi _{2,2}\\{\frac {1}{2}}~(\varphi _{1,2}+\varphi _{2,1})\end{bmatrix}}}$

For the shear terms

${\displaystyle {\begin{bmatrix}Q_{1}\\Q_{2}\end{bmatrix}}={\cfrac {\kappa }{2}}\left\{\int _{-h}^{h}{\begin{bmatrix}C_{55}&0\\0&C_{44}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}w_{,1}^{0}-\varphi _{1}\\w_{,2}^{0}-\varphi _{2}\end{bmatrix}}}$

The extensional stiffnesses are the quantities

${\displaystyle A_{\alpha \beta }:=\int _{-h}^{h}C_{\alpha \beta }~dx_{3}}$

The bending stiffnesses are the quantities

${\displaystyle D_{\alpha \beta }:=\int _{-h}^{h}x_{3}^{2}~C_{\alpha \beta }~dx_{3}}$

Isotropic and homogeneous Uflyand-Mindlin plates

Main article: Mindlin–Reissner plate theory

For uniformly thick, homogeneous, and isotropic plates, the stress–strain relations in the plane of the plate are

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.}$

where ${\displaystyle E}$ is the Young's modulus, ${\displaystyle \nu }$ is the Poisson's ratio, and ${\displaystyle \varepsilon _{\alpha \beta }}$ are the in-plane strains. The through-the-thickness shear stresses and strains are related by

${\displaystyle \sigma _{31}=2G\varepsilon _{31}\quad {\text{and}}\quad \sigma _{32}=2G\varepsilon _{32}}$

where ${\displaystyle G=E/(2(1+\nu ))}$ is the shear modulus.

Constitutive relations

The relations between the stress resultants and the generalized displacements for an isotropic Mindlin–Reissner plate are:

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}={\cfrac {2Eh}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}\,,}$

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2Eh^{3}}{3(1-\nu ^{2})}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varphi _{1,1}\\\varphi _{2,2}\\{\frac {1}{2}}(\varphi _{1,2}+\varphi _{2,1})\end{bmatrix}}\,,}$

and

${\displaystyle {\begin{bmatrix}Q_{1}\\Q_{2}\end{bmatrix}}=\kappa Gh{\begin{bmatrix}w_{,1}^{0}-\varphi _{1}\\w_{,2}^{0}-\varphi _{2}\end{bmatrix}}\,.}$

The bending rigidity is defined as the quantity

${\displaystyle D={\cfrac {2Eh^{3}}{3(1-\nu ^{2})}}\,.}$

For a plate of thickness ${\displaystyle H}$, the bending rigidity has the form

${\displaystyle D={\cfrac {EH^{3}}{12(1-\nu ^{2})}}\,.}$

where ${\displaystyle h={\frac {H}{2}}}$

Governing equations

If we ignore the in-plane extension of the plate, the governing equations are

${\displaystyle {\begin{aligned}M_{\alpha \beta ,\beta }-Q_{\alpha }&=0\\Q_{\alpha ,\alpha }+q&=0\,.\end{aligned}}}$

In terms of the generalized deformations ${\displaystyle w^{0},\varphi _{1},\varphi _{2}}$, the three governing equations are

${\displaystyle {\begin{aligned}&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)=-{\frac {q}{D}}\\&\nabla ^{2}w^{0}-{\frac {\partial \varphi _{1}}{\partial x_{1}}}-{\frac {\partial \varphi _{2}}{\partial x_{2}}}=-{\frac {q}{\kappa Gh}}\\&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)=-{\frac {2\kappa Gh}{D(1-\nu )}}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)\,.\end{aligned}}}$

The boundary conditions along the edges of a rectangular plate are

${\displaystyle {\begin{aligned}{\text{simply supported}}\quad &\quad w^{0}=0,M_{11}=0~({\text{or}}~M_{22}=0),\varphi _{1}=0~({\text{or}}~\varphi _{2}=0)\\{\text{clamped}}\quad &\quad w^{0}=0,\varphi _{1}=0,\varphi _{2}=0\,.\end{aligned}}}$

Reissner–Stein static theory for isotropic cantilever plates

In general, exact solutions for cantilever plates using plate theory are quite involved and few exact solutions can be found in the literature. Reissner and Stein ^[7] provide a simplified theory for cantilever plates that is an improvement over older theories such as Saint-Venant plate theory.

The Reissner-Stein theory assumes a transverse displacement field of the form

${\displaystyle w(x,y)=w_{x}(x)+y\,\theta _{x}(x)\,.}$

The governing equations for the plate then reduce to two coupled ordinary differential equations:

${\displaystyle {\begin{aligned}&bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=q_{1}(x)-n_{1}(x){\cfrac {d^{2}w_{x}}{dx^{2}}}-{\cfrac {dn_{1}}{dx}}\,{\cfrac {dw_{x}}{dx}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}\\&{\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=q_{2}(x)-n_{3}(x){\cfrac {d^{2}\theta _{x}}{dx^{2}}}-{\cfrac {dn_{3}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}\,{\cfrac {d^{2}w_{x}}{dx^{2}}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {dw_{x}}{dx}}\end{aligned}}}$

where

${\displaystyle {\begin{aligned}q_{1}(x)&=\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y~,~~q_{2}(x)=\int _{-b/2}^{b/2}y\,q(x,y)\,{\text{d}}y~,~~n_{1}(x)=\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\\n_{2}(x)&=\int _{-b/2}^{b/2}y\,n_{x}(x,y)\,{\text{d}}y~,~~n_{3}(x)=\int _{-b/2}^{b/2}y^{2}\,n_{x}(x,y)\,{\text{d}}y\,.\end{aligned}}}$

At ${\displaystyle x=0}$, since the beam is clamped, the boundary conditions are

${\displaystyle w(0,y)={\cfrac {dw}{dx}}{\Bigr |}_{x=0}=0\qquad \implies \qquad w_{x}(0)={\cfrac {dw_{x}}{dx}}{\Bigr |}_{x=0}=\theta _{x}(0)={\cfrac {d\theta _{x}}{dx}}{\Bigr |}_{x=0}=0\,.}$

The boundary conditions at ${\displaystyle x=a}$ are

${\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+n_{1}(x){\cfrac {dw_{x}}{dx}}+n_{2}(x){\cfrac {d\theta _{x}}{dx}}+q_{x1}=0\\&{\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}+\left[n_{3}(x)-2bD(1-\nu )\right]{\cfrac {d\theta _{x}}{dx}}+n_{2}(x){\cfrac {dw_{x}}{dx}}+t=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}+m_{1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}+m_{2}=0\end{aligned}}}$

where

${\displaystyle {\begin{aligned}m_{1}&=\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y~,~~m_{2}=\int _{-b/2}^{b/2}y\,m_{x}(y)\,{\text{d}}y~,~~q_{x1}=\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\\t&=q_{x2}+m_{3}=\int _{-b/2}^{b/2}y\,q_{x}(y)\,{\text{d}}y+\int _{-b/2}^{b/2}m_{xy}(y)\,{\text{d}}y\,.\end{aligned}}}$

Derivation of Reissner–Stein cantilever plate equations

The strain energy of bending of a thin rectangular plate of uniform thickness ${\displaystyle h}$ is given by ${\displaystyle U={\frac {1}{2}}\int _{0}^{a}\int _{-b/2}^{b/2}D\left\{\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)^{2}+2(1-\nu )\left[\left({\frac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\frac {\partial ^{2}w}{\partial x^{2}}}{\frac {\partial ^{2}w}{\partial y^{2}}}\right]\right\}{\text{d}}x{\text{d}}y}$ where ${\displaystyle w}$ is the transverse displacement, ${\displaystyle a}$ is the length, ${\displaystyle b}$ is the width, ${\displaystyle \nu }$ is the Poisson's ratio, ${\displaystyle E}$ is the Young's modulus, and ${\displaystyle D={\frac {Eh^{3}}{12(1-\nu )}}.}$ The potential energy of transverse loads ${\displaystyle q(x,y)}$ (per unit length) is ${\displaystyle P_{q}=\int _{0}^{a}\int _{-b/2}^{b/2}q(x,y)\,w(x,y)\,{\text{d}}x{\text{d}}y\,.}$ The potential energy of in-plane loads ${\displaystyle n_{x}(x,y)}$ (per unit width) is ${\displaystyle P_{n}={\frac {1}{2}}\int _{0}^{a}\int _{-b/2}^{b/2}n_{x}(x,y)\,\left({\frac {\partial w}{\partial x}}\right)^{2}\,{\text{d}}x{\text{d}}y\,.}$ The potential energy of tip forces ${\displaystyle q_{x}(y)}$ (per unit width), and bending moments ${\displaystyle m_{x}(y)}$ and ${\displaystyle m_{xy}(y)}$ (per unit width) is ${\displaystyle P_{t}=\int _{-b/2}^{b/2}\left(q_{x}(y)\,w(x,y)-m_{x}(y)\,{\frac {\partial w}{\partial x}}+m_{xy}(y)\,{\frac {\partial w}{\partial y}}\right){\text{d}}x{\text{d}}y\,.}$ A balance of energy requires that the total energy is ${\displaystyle W=U-(P_{q}+P_{n}+P_{t})\,.}$ 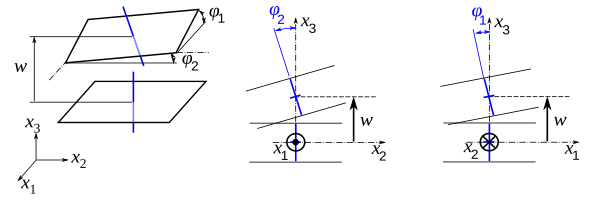With the Reissener–Stein assumption for the displacement, we have ${\displaystyle U=\int _{0}^{a}{\frac {bD}{24}}\left[12\left({\cfrac {d^{2}w_{x}}{dx^{2}}}\right)^{2}+b^{2}\left({\cfrac {d^{2}\theta _{x}}{dx^{2}}}\right)^{2}+24(1-\nu )\left({\cfrac {d\theta _{x}}{dx}}\right)^{2}\right]\,{\text{d}}x\,,}$ ${\displaystyle P_{q}=\int _{0}^{a}\left[\left(\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y\right)w_{x}+\left(\int _{-b/2}^{b/2}yq(x,y)\,{\text{d}}y\right)\theta _{x}\right]\,dx\,,}$ ${\displaystyle {\begin{aligned}P_{n}&={\frac {1}{2}}\int _{0}^{a}\left[\left(\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\right)\left({\cfrac {dw_{x}}{dx}}\right)^{2}+\left(\int _{-b/2}^{b/2}yn_{x}(x,y)\,{\text{d}}y\right){\cfrac {dw_{x}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}\right.\\&\left.\qquad \qquad +\left(\int _{-b/2}^{b/2}y^{2}n_{x}(x,y)\,{\text{d}}y\right)\left({\cfrac {d\theta _{x}}{dx}}\right)^{2}\right]{\text{d}}x\,,\end{aligned}}}$ and ${\displaystyle {\begin{aligned}P_{t}&=\left(\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\right)w_{x}-\left(\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y\right){\cfrac {dw_{x}}{dx}}+\left[\int _{-b/2}^{b/2}\left(yq_{x}(y)+m_{xy}(y)\right)\,{\text{d}}y\right]\theta _{x}\\&\qquad \qquad -\left(\int _{-b/2}^{b/2}ym_{x}(y)\,{\text{d}}y\right){\cfrac {d\theta _{x}}{dx}}\,.\end{aligned}}}$ Taking the first variation of ${\displaystyle W}$ with respect to ${\displaystyle (w_{x},\theta _{x},x)}$ and setting it to zero gives us the Euler equations ${\displaystyle {\text{(1)}}\qquad bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=q_{1}(x)-n_{1}(x){\cfrac {d^{2}w_{x}}{dx^{2}}}-{\cfrac {dn_{1}}{dx}}\,{\cfrac {dw_{x}}{dx}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}}$ and ${\displaystyle {\text{(2)}}\qquad {\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=q_{2}(x)-n_{3}(x){\cfrac {d^{2}\theta _{x}}{dx^{2}}}-{\cfrac {dn_{3}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}\,{\cfrac {d^{2}w_{x}}{dx^{2}}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {dw_{x}}{dx}}}$ where ${\displaystyle {\begin{aligned}q_{1}(x)&=\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y~,~~q_{2}(x)=\int _{-b/2}^{b/2}y\,q(x,y)\,{\text{d}}y~,~~n_{1}(x)=\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\\n_{2}(x)&=\int _{-b/2}^{b/2}y\,n_{x}(x,y)\,{\text{d}}y~,~~n_{3}(x)=\int _{-b/2}^{b/2}y^{2}\,n_{x}(x,y)\,{\text{d}}y.\end{aligned}}}$ Since the beam is clamped at ${\displaystyle x=0}$, we have ${\displaystyle w(0,y)={\cfrac {dw}{dx}}{\Bigr |}_{x=0}=0\qquad \implies \qquad w_{x}(0)={\cfrac {dw_{x}}{dx}}{\Bigr |}_{x=0}=\theta _{x}(0)={\cfrac {d\theta _{x}}{dx}}{\Bigr |}_{x=0}=0\,.}$ The boundary conditions at ${\displaystyle x=a}$ can be found by integration by parts: ${\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+n_{1}(x){\cfrac {dw_{x}}{dx}}+n_{2}(x){\cfrac {d\theta _{x}}{dx}}+q_{x1}=0\\&{\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}+\left[n_{3}(x)-2bD(1-\nu )\right]{\cfrac {d\theta _{x}}{dx}}+n_{2}(x){\cfrac {dw_{x}}{dx}}+t=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}+m_{1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}+m_{2}=0\end{aligned}}}$ where ${\displaystyle {\begin{aligned}m_{1}&=\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y~,~~m_{2}=\int _{-b/2}^{b/2}y\,m_{x}(y)\,{\text{d}}y~,~~q_{x1}=\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\\t&=q_{x2}+m_{3}=\int _{-b/2}^{b/2}y\,q_{x}(y)\,{\text{d}}y+\int _{-b/2}^{b/2}m_{xy}(y)\,{\text{d}}y.\end{aligned}}}$

See also

• Bending of plates
• Vibration of plates
• Infinitesimal strain theory
• Membrane theory of shells
• Finite strain theory
• Stress (mechanics)
• Stress resultants
• Linear elasticity
• Bending
• Föppl–von Kármán equations
• Euler–Bernoulli beam equation
• Timoshenko beam theory

References

1. Timoshenko, S. and Woinowsky-Krieger, S. "Theory of plates and shells". McGraw–Hill New York, 1959.
2. A. E. H. Love, On the small free vibrations and deformations of elastic shells, Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 p. 491–549.
3. Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis.
4. Uflyand, Ya. S.,1948, Wave Propagation by Transverse Vibrations of Beams and Plates, PMM: Journal of Applied Mathematics and Mechanics, Vol. 12, 287-300 (in Russian)
5. Elishakoff ,I.,2020, Handbook on Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate Theories, World Scientific, Singapore, ISBN   978-981-3236-51-6
6. R. D. Mindlin, Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, Journal of Applied Mechanics, 1951, Vol. 18 p. 31–38.
7. E. Reissner and M. Stein. Torsion and transverse bending of cantilever plates. Technical Note 2369, National Advisory Committee for Aeronautics,Washington, 1951.