
The boiling point of a substance is the temperature at which the vapor pressure of a liquid equals the pressure surrounding the liquid and the liquid changes into a vapor.

Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, quantum chemistry, statistical mechanics, analytical dynamics and chemical equilibria.

In chemistry, a solution is defined by IUPAC as "A liquid or solid phase containing more than one substance, when for convenience one substance, which is called the solvent, is treated differently from the other substances, which are called solutes. When, as is often but not necessarily the case, the sum of the mole fractions of solutes is small compared with unity, the solution is called a dilute solution. A superscript attached to the ∞ symbol for a property of a solution denotes the property in the limit of infinite dilution." One important parameter of a solution is the concentration, which is a measure of the amount of solute in a given amount of solution or solvent. The term "aqueous solution" is used when one of the solvents is water.

In thermodynamics, the enthalpy of vaporization, also known as the (latent) heat of vaporization or heat of evaporation, is the amount of energy (enthalpy) that must be added to a liquid substance to transform a quantity of that substance into a gas. The enthalpy of vaporization is a function of the pressure and temperature at which the transformation takes place.

Vapor pressure or equilibrium vapor pressure is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases at a given temperature in a closed system. The equilibrium vapor pressure is an indication of a liquid's thermodynamic tendency to evaporate. It relates to the balance of particles escaping from the liquid in equilibrium with those in a coexisting vapor phase. A substance with a high vapor pressure at normal temperatures is often referred to as volatile. The pressure exhibited by vapor present above a liquid surface is known as vapor pressure. As the temperature of a liquid increases, the attractive interactions between liquid molecules become less significant in comparison to the entropy of those molecules in the gas phase, increasing the vapor pressure. Thus, liquids with strong intermolecular interactions are likely to have smaller vapor pressures, with the reverse true for weaker interactions.
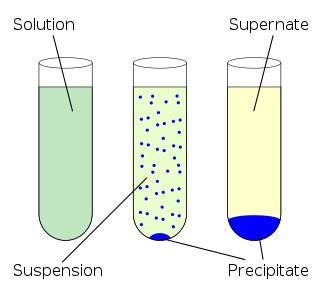
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.

Freezing-point depression is a drop in the maximum temperature at which a substance freezes, caused when a smaller amount of another, non-volatile substance is added. Examples include adding salt into water, alcohol in water, ethylene or propylene glycol in water, adding copper to molten silver, or the mixing of two solids such as impurities into a finely powdered drug.

Thermodynamic databases contain information about thermodynamic properties for substances, the most important being enthalpy, entropy, and Gibbs free energy. Numerical values of these thermodynamic properties are collected as tables or are calculated from thermodynamic datafiles. Data is expressed as temperature-dependent values for one mole of substance at the standard pressure of 101.325 kPa, or 100 kPa. Both of these definitions for the standard condition for pressure are in use.
In thermodynamics and chemical engineering, the vapor–liquid equilibrium (VLE) describes the distribution of a chemical species between the vapor phase and a liquid phase.

In statistical thermodynamics, the UNIFAC method is a semi-empirical system for the prediction of non-electrolyte activity in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients. By using interactions for each of the functional groups present on the molecules, as well as some binary interaction coefficients, the activity of each of the solutions can be calculated. This information can be used to obtain information on liquid equilibria, which is useful in many thermodynamic calculations, such as chemical reactor design, and distillation calculations.
The Joback method, often named Joback–Reid method, predicts eleven important and commonly used pure component thermodynamic properties from molecular structure only. It is named after Kevin G. Joback in 1984 and developed it further with Robert C. Reid. The Joback method is an extension of the Lydersen method and uses very similar groups, formulas, and parameters for the three properties the Lydersen already supported.
The lower critical solution temperature (LCST) or lower consolute temperature is the critical temperature below which the components of a mixture are miscible in all proportions. The word lower indicates that the LCST is a lower bound to a temperature interval of partial miscibility, or miscibility for certain compositions only.

In statistical thermodynamics, UNIQUAC is an activity coefficient model used in description of phase equilibria. The model is a so-called lattice model and has been derived from a first order approximation of interacting molecule surfaces. The model is, however, not fully thermodynamically consistent due to its two-liquid mixture approach. In this approach the local concentration around one central molecule is assumed to be independent from the local composition around another type of molecule.
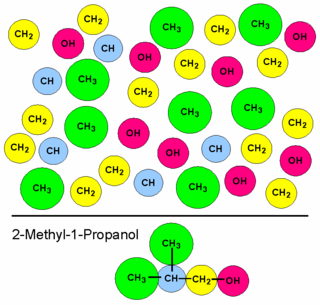
In thermodynamic modelling, the Klincewicz method is a predictive method based both on group contributions and on a correlation with some basic molecular properties. The method estimates the critical temperature, the critical pressure, and the critical volume of pure components. It is named after Karen Klincewicz Gleason who developed it in 1984 in collaboration with Robert C. Reid.
PSRK is an estimation method for the calculation of phase equilibria of mixtures of chemical components. The original goal for the development of this method was to enable the estimation of properties of mixtures containing supercritical components. This class of substances cannot be predicted with established models, for example UNIFAC.
The Girolami method, named after Gregory Girolami, is a predictive method for estimating densities of pure liquid components at room temperature. The objective of this method is the simple prediction of the density and not high precision.
The Lydersen method is a group contribution method for the estimation of critical properties temperature (Tc), pressure (Pc) and volume (Vc). The method is named after Aksel Lydersen who published it in 1955. The Lydersen method is the prototype for and ancestor of many new models like Joback, Klincewicz, Ambrose, Gani-Constantinou and others.
VTPR is an estimation method for the calculation of phase equilibria of mixtures of chemical components. The original goal for the development of this method was to enable the estimation of properties of mixtures which contain supercritical components. These class of substances couldn't be predicted with established models like UNIFAC.
Toxic units (TU) are used in the field of toxicology to quantify the interactions of toxicants in binary mixtures of chemicals. A toxic unit for a given compound is based on the concentration at which there is a 50% effect for a certain biological endpoint. One toxic unit is equal to the EC50 for a given endpoint for a specific biological effect over a given amount of time. Toxic units allow for the comparison of the individual toxicities of a binary mixture to the combined toxicity. This allows researchers to categorize mixtures as additive, synergistic or antagonistic. Synergism and antagonism are defined by mixtures that are more or less toxic than predicted by the sum of their toxic units.
Deresh RamjugernathFAAS is a South African professor of Engineering Technology & Applied Sciences. He was a Deputy Vice-Chancellor of Research at the University of KwaZulu-Natal (UKZN) and will assume the position Rector and Vice-Chancellor at Stellenbosch University on 1 April 2025.
















