| Hemitesseract (hemi-4-cube) | |
|---|---|
 | |
| Type | Regular projective 4-polytope |
| Schläfli symbol | {4,3,3}/2 or {4,3,3}4 |
| Cells | 4 {4,3}  |
| Faces | 12 {4} |
| Edges | 16 |
| Vertices | 8 |
| Vertex figure | Tetrahedron |
| Petrie polygon | Square |
| Dual | hemi-16-cell |
In abstract geometry, a hemitesseract is an abstract, regular polyhedron, containing half the cells of a tesseract, existing in real projective space, RP3. [1]
It has four cubic cells, 12 square faces, 16 edges, and 8 vertices. It has an unexpected property that every cell is in contact with every other cell on two faces, and every cell contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets.
 |  |  |
| In a cubic projection, the 4 cubic cells can be seen by selecting 3 of 4 sets of parallel edges. One is direct,and three are seen as cross-cubes. One of 6 square faces is shown yellow in each cube. | A projection inside a regular octagon, with two colors of vertices showing it as complete bipartite graph K4,4, and its 4 sets of 4 parallel edges. | |
From the point of view of graph theory, the skeleton is a cubic graph with 8 diagonal central edges added.
It is also the complete bipartite graph K4,4, and the regular complex polygon 2{4}4, a generalized cross polytope.[ clarification needed ]
This configuration matrix represents the hemitesseract. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole hemitesseract. The nondiagonal numbers say how many of the column's element occur in or at the row's element. [2] For example, the 2 in the first column of the second row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 4 in the second column of the first row indicates that 4 edges meet at each vertex.
In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as the rectangular cuboid with six faces are all squares, and parallelepiped with the edges are all equal. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.
In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol {3,3,3}. It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4-simplex (Coxeter's polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides.
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].
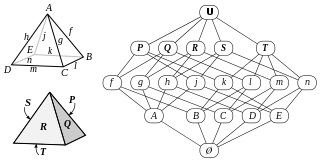
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube (penteract) with alternated vertices removed.
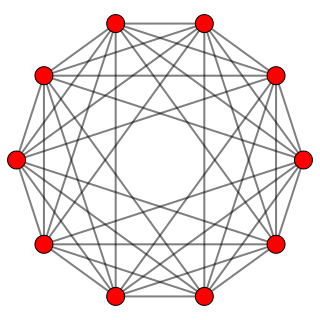
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(1/5), or approximately 78.46°.
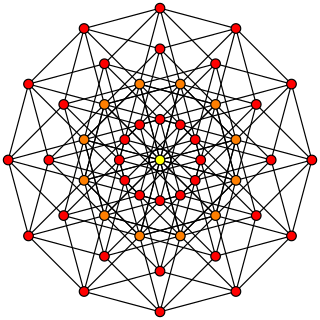
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.
In geometry, a 6-orthoplex, or 6-cross polytope, is a regular 6-polytope with 12 vertices, 60 edges, 160 triangle faces, 240 tetrahedron cells, 192 5-cell 4-faces, and 64 5-faces.
In geometry, a 6-demicube or demihexeract is a uniform 6-polytope, constructed from a 6-cube (hexeract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces.
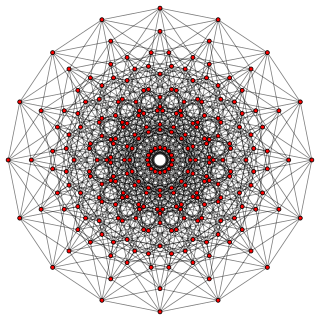
In geometry, an 8-cube is an eight-dimensional hypercube. It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.
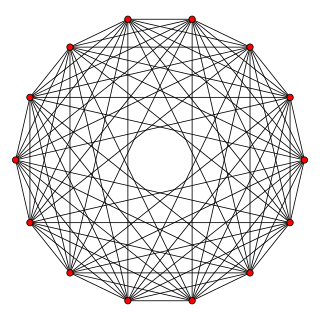
In geometry, a 7-orthoplex, or 7-cross polytope, is a regular 7-polytope with 14 vertices, 84 edges, 280 triangle faces, 560 tetrahedron cells, 672 5-cells 4-faces, 448 5-faces, and 128 6-faces.
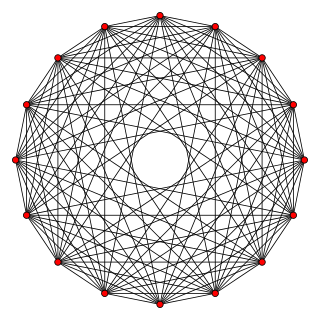
In geometry, an 8-orthoplex or 8-cross polytope is a regular 8-polytope with 16 vertices, 112 edges, 448 triangle faces, 1120 tetrahedron cells, 1792 5-cells 4-faces, 1792 5-faces, 1024 6-faces, and 256 7-faces.
In five-dimensional geometry, a rectified 5-simplex is a convex uniform 5-polytope, being a rectification of the regular 5-simplex.
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
In geometry, H. S. M. Coxeter called a regular polytope a special kind of configuration.
