In geometry, a cuboid is a convex polyhedron bounded by six quadrilateral faces, whose polyhedral graph is the same as that of a cube. While mathematical literature refers to any such polyhedron as a cuboid, other sources use "cuboid" to refer to a shape of this type in which each of the faces is a rectangle ; this more restrictive type of cuboid is also known as a rectangular cuboid, right cuboid, rectangular box, rectangular hexahedron, right rectangular prism, or rectangular parallelepiped.

In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.

In geometry, a hendecagon or 11-gon is an eleven-sided polygon.

In geometry, the square orthobicupola is one of the Johnson solids (J28). As the name suggests, it can be constructed by joining two square cupolae (J4) along their octagonal bases, matching like faces. A 45-degree rotation of one cupola before the joining yields a square gyrobicupola (J29).
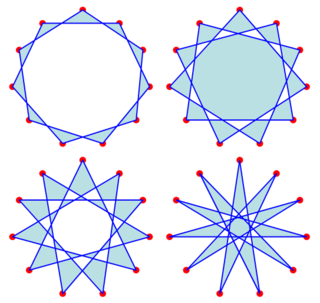
In geometry, a hendecagram is a star polygon that has eleven vertices.

In geometry, the augmented hexagonal prism is one of the Johnson solids (J54). As the name suggests, it can be constructed by augmenting a hexagonal prism by attaching a square pyramid (J1) to one of its equatorial faces. When two or three such pyramids are attached, the result may be a parabiaugmented hexagonal prism, a metabiaugmented hexagonal prism or a triaugmented hexagonal prism.

In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are 2 (polygon) or higher.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.
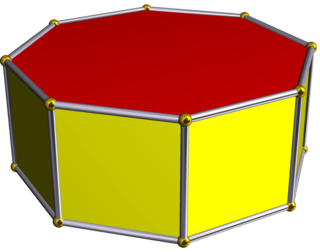
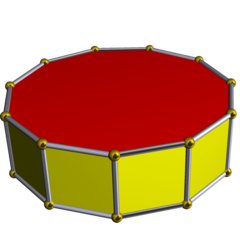
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.
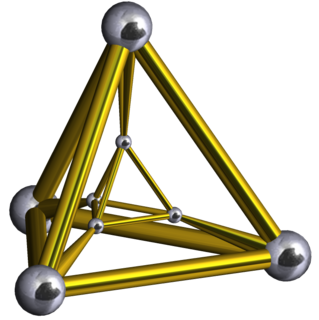
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices.

In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a p-gonal antiprismatic prism is [2p,2+,2], order 8p.

The wedge prism is a prism with a shallow angle between its input and output surfaces. This angle is usually 3 degrees or less. Refraction at the surfaces causes the prism to deflect light by a fixed angle. When viewing a scene through such a prism, objects will appear to be offset by an amount that varies with their distance from the prism.

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.
In geometry, an icosidigon or 22-gon is a twenty-two-sided polygon. The sum of any icosidigon's interior angles is 3600 degrees.