In geometry, the triaugmented triangular prism or tetracaidecadeltahedron is one of the Johnson solids (J51). As the name suggests, it can be constructed by attaching square pyramids (J1) to each of the three equatorial faces of the triangular prism. It is a deltahedron.
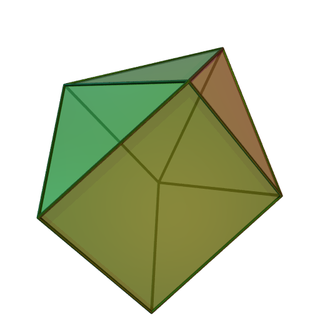
In geometry, the augmented triangular prism is one of the Johnson solids (J49). As the name suggests, it can be constructed by augmenting a triangular prism by attaching a square pyramid (J1) to one of its equatorial faces. The resulting solid bears a superficial resemblance to the gyrobifastigium (J26), the difference being that the latter is constructed by attaching a second triangular prism, rather than a square pyramid.

In geometry, the biaugmented triangular prism is one of the Johnson solids (J50). As the name suggests, it can be constructed by augmenting a triangular prism by attaching square pyramids (J1) to two of its equatorial faces.

In geometry, the biaugmented pentagonal prism is one of the Johnson solids (J53). As the name suggests, it can be constructed by doubly augmenting a pentagonal prism by attaching square pyramids (J1) to two of its nonadjacent equatorial faces.

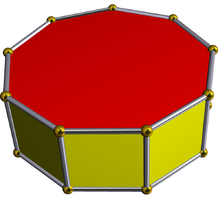
In geometry, the augmented hexagonal prism is one of the Johnson solids (J54). As the name suggests, it can be constructed by augmenting a hexagonal prism by attaching a square pyramid (J1) to one of its equatorial faces. When two or three such pyramids are attached, the result may be a parabiaugmented hexagonal prism, a metabiaugmented hexagonal prism or a triaugmented hexagonal prism.

In geometry, the parabiaugmented hexagonal prism is one of the Johnson solids (J55). As the name suggests, it can be constructed by doubly augmenting a hexagonal prism by attaching square pyramids (J1) to two of its nonadjacent, parallel (opposite) equatorial faces. Attaching the pyramids to nonadjacent, nonparallel equatorial faces yields a metabiaugmented hexagonal prism.

In geometry, the metabiaugmented hexagonal prism is one of the Johnson solids (J56). As the name suggests, it can be constructed by doubly augmenting a hexagonal prism by attaching square pyramids (J1) to two of its nonadjacent, nonparallel equatorial faces. Attaching the pyramids to opposite equatorial faces yields a parabiaugmented hexagonal prism.

In geometry, the triaugmented hexagonal prism is one of the Johnson solids (J57). As the name suggests, it can be constructed by triply augmenting a hexagonal prism by attaching square pyramids (J1) to three of its nonadjacent equatorial faces.

In geometry, a uniform 4-polytope is a 4-polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are 2 (polygon) or higher.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.

In geometry, the hexagonal prism is a prism with hexagonal base. This polyhedron has 8 faces, 18 edges, and 12 vertices.
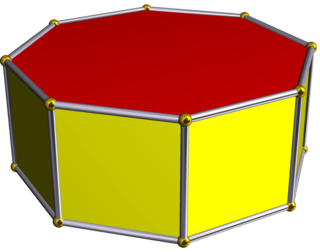
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.

In geometry, the decagonal prism is the eighth in the infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra. The decagonal prism has 12 faces, 30 edges, and 20 vertices. If faces are all regular, it is a semiregular or prismatic uniform polyhedron.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.