Decagonal prism

Last updated
Uniform Decagonal prism
Decagonal prism.png
Type Prismatic uniform polyhedron
Elements F = 12, E = 30, V = 20 (χ = 2)
Faces by sides10{4}+2{10}
Schläfli symbol t{2,10} or {10}x{}
Wythoff symbol 2 10 | 2
2 2 5 |
Coxeter diagrams CDel node 1.pngCDel 2.pngCDel node 1.pngCDel 10.pngCDel node.png
CDel node 1.pngCDel 2.pngCDel node 1.pngCDel 5.pngCDel node 1.png
CDel node 1.pngCDel 2.pngCDel node h.pngCDel 10.pngCDel node h.png
CDel node h.pngCDel 2x.pngCDel node h.pngCDel 10.pngCDel node 1.png
Symmetry D10h, [10,2], (*10.2.2), order 40
Rotation group D10, [10,2]+, (10.2.2), order 20
References U 76(h)
Dual Decagonal dipyramid
Properties convex, zonohedron
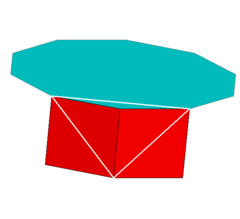
Decagonal prism vf.png
Vertex figure
4.4.10

In geometry, the decagonal prism is the eighth in the infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra. The decagonal prism has 12 faces, 30 edges, and 20 vertices. If faces are all regular, it is a semiregular or prismatic uniform polyhedron.

Geometry branch of mathematics that measures the shape, size and position of objects

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Prism (geometry) geometric shape, a polyhedron with an n-sided polygonal base

In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.

Decagon shape with ten sides

In geometry, a decagon is a ten-sided polygon or 10-gon.

Contents

Uses

The decagonal prism exists as cells in two four-dimensional uniform 4-polytopes:

Uniform 4-polytope 4-polytope which has uniform polyhedra as cells and is vertex-transitive

In geometry, a uniform 4-polytope is a 4-polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

Runcitruncated 120-cell
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 3.pngCDel node 1.png		 Omnitruncated 120-cell
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.pngCDel 3.pngCDel node 1.png
120-cell t013 H3.png 120-cell t0123 H3.png
Family of uniform prisms
Polyhedron Yellow square.gif Triangular prism.png Tetragonal prism.png Pentagonal prism.png Hexagonal prism.png Prism 7.png Octagonal prism.png Prism 9.png Decagonal prism.png Hendecagonal prism.png Dodecagonal prism.png
Coxeter CDel node 1.pngCDel 2.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 3.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 4.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 5.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 6.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 7.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 8.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 9.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 10.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 11.pngCDel node.pngCDel 2.pngCDel node 1.pngCDel node 1.pngCDel 12.pngCDel node.pngCDel 2.pngCDel node 1.png
Tiling Tetragonal dihedron.png Spherical triangular prism.png Spherical square prism.png Spherical pentagonal prism.png Spherical hexagonal prism.png Spherical heptagonal prism.png Spherical octagonal prism.png Spherical decagonal prism.png
Config. 2.4.4 3.4.4 4.4.4 5.4.4 6.4.4 7.4.4 8.4.4 9.4.4 10.4.4 11.4.4 12.4.4

Eric Wolfgang Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science (ScienceWorld). He is the author of the CRC Concise Encyclopedia of Mathematics. He currently works for Wolfram Research, Inc.

MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Related Research Articles

Gyroelongated pentagonal rotunda Johnson solid

In geometry, the gyroelongated pentagonal rotunda is one of the Johnson solids (J25). As the name suggests, it can be constructed by gyroelongating a pentagonal rotunda (J6) by attaching a decagonal antiprism to its base. It can also be seen as a gyroelongated pentagonal birotunda (J48) with one pentagonal rotunda removed.

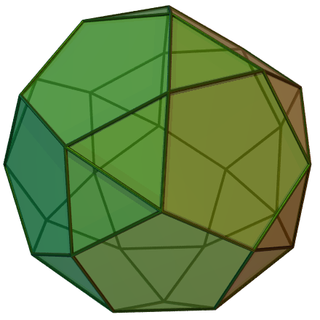
Pentagonal orthobirotunda Johnson solid

In geometry, the pentagonal orthobirotunda is one of the Johnson solids (J34). It can be constructed by joining two pentagonal rotundae (J6) along their decagonal faces, matching like faces.

Elongated pentagonal gyrobirotunda Johnson solid

In geometry, the elongated pentagonal gyrobirotunda is one of the Johnson solids (J43). As the name suggests, it can be constructed by elongating a "pentagonal gyrobirotunda," or icosidodecahedron, by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae (J6) through 36 degrees before inserting the prism yields an elongated pentagonal orthobirotunda (J42).

Elongated pentagonal orthobirotunda Johnson solid

In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids (J42). Its Conway polyhedron notation is at5jP5. As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda (J34) by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae (J6) through 36 degrees before inserting the prism yields the elongated pentagonal gyrobirotunda (J43).

Gyroelongated pentagonal birotunda Johnson solid

In geometry, the gyroelongated pentagonal birotunda is one of the Johnson solids (J48). As the name suggests, it can be constructed by gyroelongating a pentagonal birotunda by inserting a decagonal antiprism between its two halves.

Gyroelongated pentagonal cupola Johnson solid

In geometry, the gyroelongated pentagonal cupola is one of the Johnson solids (J24). As the name suggests, it can be constructed by gyroelongating a pentagonal cupola (J5) by attaching a decagonal antiprism to its base. It can also be seen as a gyroelongated pentagonal bicupola (J46) with one pentagonal cupola removed.

Elongated pentagonal orthobicupola Johnson solid

In geometry, the elongated pentagonal orthobicupola is one of the Johnson solids (J38). As the name suggests, it can be constructed by elongating a pentagonal orthobicupola (J30) by inserting a decagonal prism between its two congruent halves. Rotating one of the cupolae through 36 degrees before inserting the prism yields an elongated pentagonal gyrobicupola (J39).

Elongated pentagonal gyrobicupola Johnson solid

In geometry, the elongated pentagonal gyrobicupola is one of the Johnson solids (J39). As the name suggests, it can be constructed by elongating a pentagonal gyrobicupola (J31) by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal cupolae (J5) through 36 degrees before inserting the prism yields an elongated pentagonal orthobicupola (J38).

Gyroelongated pentagonal bicupola Johnson solid

In geometry, the gyroelongated pentagonal bicupola is one of the Johnson solids (J46). As the name suggests, it can be constructed by gyroelongating a pentagonal bicupola by inserting a decagonal antiprism between its congruent halves.

Elongated pentagonal gyrocupolarotunda Johnson solid

In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids (J41). As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda (J33) by inserting a decagonal prism between its halves. Rotating either the pentagonal cupola (J5) or the pentagonal rotunda (J6) through 36 degrees before inserting the prism yields an elongated pentagonal orthocupolarotunda (J40).

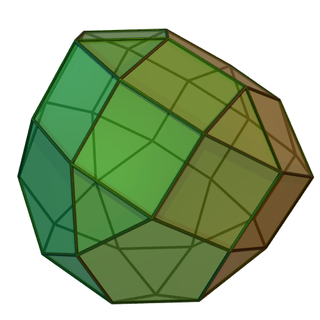
Elongated pentagonal orthocupolarotunda Johnson solid

In geometry, the elongated pentagonal orthocupolarotunda is one of the Johnson solids (J40). As the name suggests, it can be constructed by elongating a pentagonal orthocupolarotunda (J32) by inserting a decagonal prism between its halves. Rotating either the cupola or the rotunda through 36 degrees before inserting the prism yields an elongated pentagonal gyrocupolarotunda (J41).

Gyroelongated pentagonal cupolarotunda Johnson solid

In geometry, the gyroelongated pentagonal cupolarotunda is one of the Johnson solids (J47). As the name suggests, it can be constructed by gyroelongating a pentagonal cupolarotunda by inserting a decagonal antiprism between its two halves.

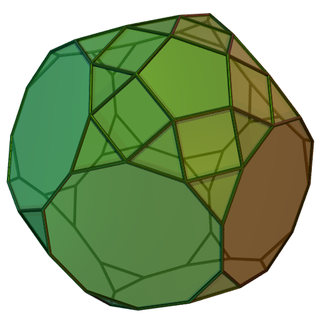
Augmented truncated dodecahedron Johnson solid

In geometry, the augmented truncated dodecahedron is one of the Johnson solids (J68). As its name suggests, it is created by attaching a pentagonal cupola (J5) onto one decagonal face of a truncated dodecahedron.

Parabiaugmented truncated dodecahedron Johnson solid

In geometry, the parabiaugmented truncated dodecahedron is one of the Johnson solids (J69). As its name suggests, it is created by attaching two pentagonal cupolas (J5) onto two parallel decagonal faces of a truncated dodecahedron.

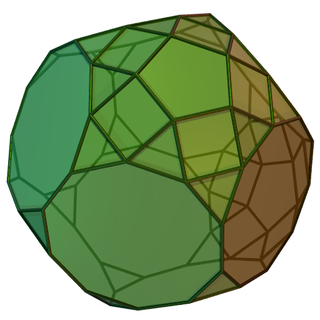
Metabiaugmented truncated dodecahedron Johnson solid

In geometry, the metabiaugmented truncated dodecahedron is one of the Johnson solids (J70). As its name suggests, it is created by attaching two pentagonal cupolas (J5) onto two nonadjacent, nonparallel decagonal faces of a truncated dodecahedron.

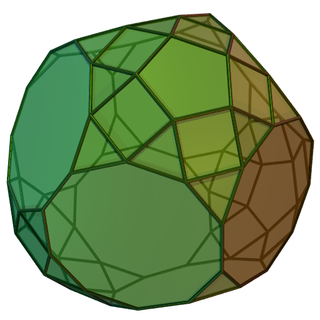
Triaugmented truncated dodecahedron Johnson solid

In geometry, the triaugmented truncated dodecahedron is one of the Johnson solids (J71); of them, it has the greatest volume in proportion to the cube of the side length. As its name suggests, it is created by attaching three pentagonal cupolas (J5) onto three nonadjacent decagonal faces of a truncated dodecahedron.

Dodecahedral prism convex uniform 4-polytope

In geometry, a dodecahedral prism is a convex uniform 4-polytope. This 4-polytope has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices.

Runcinated 120-cells

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

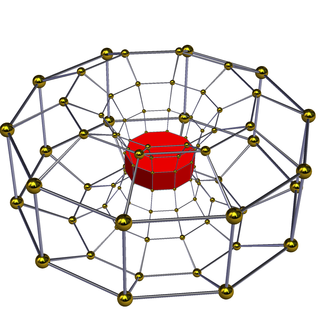
10-10 duoprism

In geometry of 4 dimensions, a 10-10 duoprism or decagonal duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two decagons.