Hipparchic cycle

The Greek astronomer Hipparchus introduced three cycles that have been named after him in later literature.

Calendar cycle

Hipparchus proposed a correction to the 76-year-long Callippic cycle, which itself was proposed as a correction to the 19-year-long Metonic cycle. He may have published it in the book "On the Length of the Year" (Περὶ ἐνιαυσίου μεγέθους), which has since been lost.

From solstice observations, Hipparchus found that the tropical year is about 1⁄300 of a day shorter than the 365+1⁄4 days that Calippus used (see Almagest III.1). So he proposed to make a 1-day correction after 4 Calippic cycles, i.e. 304 years = 3,760 lunations = 111,035 days.

Error implicit in the cycle

This is a very close approximation for an integer number of lunations in an integer number of days (with an error of only 0.014 days). However, it is in fact 1.37 days longer than 304 tropical years. The mean tropical year is actually about 1⁄128 day (11 minutes 15 seconds) shorter than the Julian calendar year of 365+1⁄4 days. These differences cannot be corrected with any cycle that is a multiple of the 19-year cycle of 235 lunations; it is an accumulation of the mismatch between years and months in the basic Metonic cycle, and the lunar months need to be shifted systematically by a day with respect to the solar year (i.e. the Metonic cycle itself needs to be corrected) after every 228 years.^{[ citation needed ]}

Indeed, from the values of the tropical year (365.2421896698 days) and the synodic month (29.530588853) cited in the respective articles of Wikipedia, it follows that the length of 228=12×19 tropical years is about 83,275.22 days, shorter than the length of 12×235 synodic months—namely about 83,276.26 days—by one day plus about one hour. In fact, an even better correction would be two days every 437 years, rather than one day every 228 years. The length of 437=23×19 tropical years (about 159,610.837 days) is shorter than that of 23×235 synodic months (about 159,612.833 days) by almost exactly two days, up to only six minutes.

Eclipse cycles

An eclipse cycle constructed by Hipparchus is described in Ptolemy's Almagest IV.2:

For from the observations he set out he [Hipparchus] shows that the smallest constant interval defining an ecliptic period in which the number of months and the amount of [lunar] motion is always the same, is 126007 days plus 1 equinoctial hour. In this interval he finds comprised 4267 months, 4573 complete returns in anomaly, and 4612 revolutions on the ecliptic less about 7½° which is the amount by which the sun’s motion falls short of 345 revolutions (here too the revolution of sun and moon is taken with respect to the fixed stars). (Hence, dividing the above number of days by the 4267 months, he finds the mean length of the [synodic] month as approximately 29;31,50,8,20 days).

— Book IV, Chapter 2, translation of Gerald Toomer ^[1]

Actually, dividing 126007 days and one hour by 4267 would give 29;31,50,8,9 in sexagesimal, whereas 29;31,50,8,20 was already used in Babylonian astronomy, possibly found by Kidinnu in the fourth century BC. This period is a multiple of a Babylonians unit of time equal to one eighteenth of a minute (3+1/3 seconds), which in sexagesimal is 0;0,0,8,20 days. (The true length of the month, 29.53058885 days, comes to 29;31,50,7,12 in sexagesimal, so the Babylonian value was correct to the nearest 3+1/3-second unit.)

Ptolemy points out that if one divides this cycle by 17, one obtains a whole number of synodic months (251) and a whole number of anomalistic months (269):

But if one were to look for the number of months [which always cover the same time-interval], not between two lunar eclipses, but merely between one conjunction or opposition and another syzygy of the same type, he would find an even smaller integer number of months containing a return in anomaly, by dividing the above numbers by 17 (which is their only common factor). This produces 251 months and 269 returns in anomaly.

— Book IV, Chapter 2

Franz Xaver Kugler in his Die Babylonische Mondrechnung claimed that the Chaldaeans could have known about this cycle of 251 months, because it falls out of their system of calculating the speed of the moon, seen in a tablet from around 100 BC. ^[2] In their system, the speed of the moon at new moon varies in a zigzag, with a period of one full moon cycle, changing by 36 arc minutes each month over a span of 251 arc minutes (see graph), and this implies that after 251 months the pattern repeats, and 269 anomalistic months will have gone by. So it is possible that Hipparchus constructed his 345-year cycle by multiplying this 20-year cycle by 17 so as to closely match an integer number of synodic months (4,267), anomalistic months (4,573), years (345), and days (a bit over 126,007). It is also close to a half-integer number of draconic months (4,630.53...), making it an eclipse period. By comparing his own eclipse observations with Babylonian records from 345 years earlier, he could verify the accuracy of the various periods that the Chaldean astronomers used.^{[ citation needed ]}

Comparison of speed of moon with values given in a Babylonian tablet, 104-103 BC

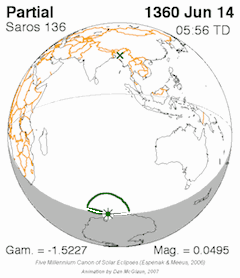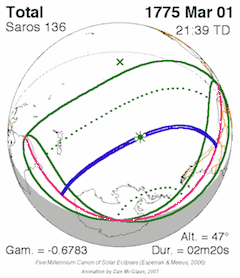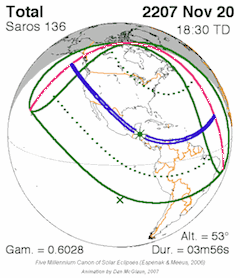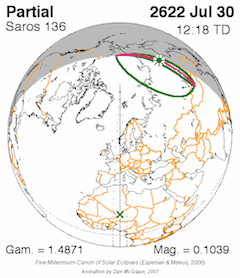
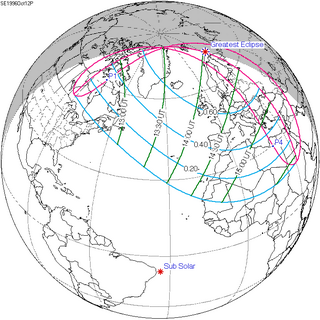
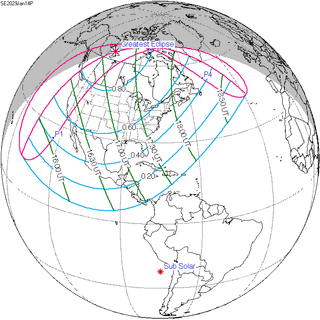
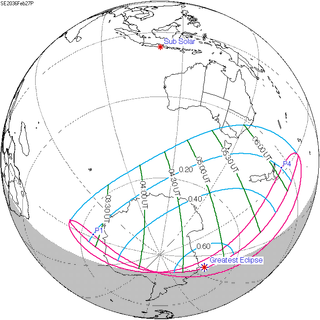
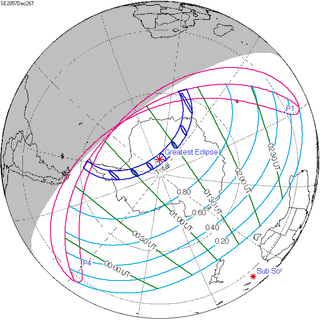
The Hipparchic eclipse cycle is made up of 25 inex minus 21 saros periods. There are only three or four eclipses in a series of eclipses separated by Hipparchic cycles. For example, the solar eclipse of August 21, 2017 was preceded by one in 1672 and will be followed by one in 2362, but there are none before or after these. ^[3]

It corresponds to:

• 4,267 synodic months
• 4,612 minus 1/48 sidereal months
• 4,630.531 draconic months
• 4,573.002 anomalistic months
• 727 eclipse seasons

There are other eclipse intervals that also have the properties desired by Hipparchus, for example an interval of 81.2 years (four of the 251-month cycles, or 19 inex minus 26 saros) which is even closer to a whole number of anomalistic months (1076.00056), and almost equally close to a half-integer number of draconic months (1089.5366). The "tritrix" eclipse cycle, ^[4] consisting of 1743 synodic months, 1891.496 draconic months, or 1867.9970 anomalistic months (140.925 years, equivalent to 3 inex plus 3 saros) is about as accurate as the interval of Hipparchus in terms of anomalistic months, but repeats many more times, around 20. An exceptionally accurate eclipse cycle from this point of view is one of 1154.5 years (43 inex minus 5 saros), which is much closer to a whole number of anomalistic months (15303.00005) than the interval of Hipparchus. At the solar eclipse of October 17, 1781, the moon had an anomaly of 0°, ^[5] and similar eclipses have occurred every 1054.5 years for more than 4000 years and will continue at least 13,000 more years. ^[6]

Comparison of length variation for three eclipse periods of exceptionally small length variability. The x-axis gives the date of the second eclipse, between 2001 and 2050. The y-axis shows the fraction of a day left after subtracting 539848, 132592, and 126007 days respectively from the 1478-, 363-, and 345-year periods. The axis on the right shows more or less the same thing, expressed as hours and minutes.

The period of Hipparchus is also accurate in the sense of always having the same length to within an hour. This is due to the fact that it is close to a whole number of anomalistic years as well as to a whole number of anomalistic months. Its average length is actually 126007.023 days, half an hour less than what Ptolemy says. This is equivalent to 345 Julian years minus 4.227 days (implying that in the Gregorian calendar the date usually goes back by just one or two days, sometimes by three), which is only about 8 days less than 345 anomalistic years. There are few eclipse periods that are so constant –the semester for example (six synodic months) can vary by a day in each direction.

Ptolemy says that Hipparchus also came up with a period of 5458 synodic months, equal to 5923 draconic months (441.3 years). This is called the Hipparchian Period, and more recently the Babylonian Period, but the latter is a misnomer as there is no evidence that the Babylonians were aware of it. ^[4] It is equivalent to 14 inex plus 2 saros periods and therefore repeats many more times than the 345-year cycle. The solar eclipse of July 11, 2010, for example, is the latest in a series that has been going for more than 13,000 years and will continue for more than 8000 more. ^[6]

References

1. Ptolemy’s ALMAGEST Translated and Annotated by G. J. Toomer (PDF). 1984. pp. 175–6. In Greek, "ἀποδείκνυσι γάρ, δι' ὧν ἐξέθετο τηρήσεων, ὅτι ὁ πρῶτος ἀριθμὸς τῶν ἡμερῶν, δι' ὅσων πάντοτε ὁ ἐκλειπτικὸς χρόνος ἐν ἴσοις μησὶν και ἐν ἴσοις κινήμασιν ἀνακυκλείται, ιβ μ ἐστιν καὶ ἔτι ͵ςζ ἡμερῶν καὶ μιᾶς ὥρας ἰσημερινῆς, ἐν αἵς μῆνας μὲν ἀπαρτιζομένους εὐρίσκει ͵δσξζ, ὅλας δὲ ἀνωμαλίας ἀποκαταστάσεις ͵δφογ, ζῳδιακοὺς δὲ κύκλους ͵δχιβ λείποντας μοίρας ζ∠ʹ ἔγγιστα, ὅσας καὶ ὁ ἥλιος εἰς τοὺς τμε κύκλους λείπει, πάλιν ὡς τῆς ἀποκαταστάσεως αὐτῶν πρὸς τοὺς ἀπλανεῖς ἀστέρας θεωρουμένης. ὅθεν εὐρίσκει καὶ τὸν μηνιαῖον μέσον χρόνον ἐπιμεριζομένου τοῦ προκειμένου τῶν ἡμερῶν πλήθους εἰς τοὺς ͵δσξζ μήνας ἡμερῶν συναγόμενον κθλανηκ ἔγγιστα." Heiberg's Edition of Ptolemy, VOL I, partes I & II, pp. 270-1. Also available here.
2. Franz Xaver Kugler (1900). Die Babylonische Mondrechnung (PDF). pp. 8–21.
3. See "Five Millennium Catalog of Solar Eclipses". NASA.
4. Rob van Gent. "A Catalogue of Eclipse Cycles - List of Eclipse Cycles". Utrecht University.
5. Giovanni Valsecchi, Ettore Perozzi, Archie Roy, Bonnie Steves (Mar 1993). "Periodic orbits close to that of the Moon". Astronomy and Astrophysics: 311.
6. Saros-Inex Panorama. Data in Solar eclipse panaorama.xls.