Octahedral pyramid

Square-pyramidal pyramid
Square-pyramidal pyramid
Type	Polyhedral pyramid
Schläfli symbol	( ) ∨ [( ) ∨ {4}] ; [( )∨( )] ∨ {4} = { } ∨ {4}; { } ∨ [{ } × { }]; { } ∨ [{ } + { }]
Cells	2 ( )∨{4} ; 4 ( )∨{3}
Faces	12 {3} ; 1 {4}
Edges	13
Vertices	6
Symmetry group	[4,1,1], order 8; [4,2,1], order 16; [2,2,1], order 8
Dual	Self-dual
Properties	convex, regular-faced

Octahedral pyramid
Octahedral pyramid
	Schlegel diagram
Type	Polyhedral pyramid
Schläfli symbol	( ) ∨ {3,4} ; ( ) ∨ r{3,3} ; ( ) ∨ s{2,6} ; ( ) ∨ [{4} + { }] ; ( ) ∨ [{ } + { } + { }]
Cells	1 {3,4} ; 8 ( ) ∨ {3}
Faces	20 {3}
Edges	18
Vertices	7
Symmetry group	B3, [4,3,1], order 48; [3,3,1], order 24; [2+,6,1], order 12; [4,2,1], order 16; [2,2,1], order 8
Dual	Cubic pyramid
Properties	convex, regular-cells, Blind polytope

Last updated October 29, 2024

In 4-dimensional geometry, the octahedral pyramid is bounded by one octahedron on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one,^[1] the triangular pyramids can be made with regular faces (as regular tetrahedrons) by computing the appropriate height.

Occurrences of the octahedral pyramid

The regular 16-cell has octahedral pyramids around every vertex, with the octahedron passing through the center of the 16-cell. Therefore placing two regular octahedral pyramids base to base constructs a 16-cell. The 16-cell tessellates 4-dimensional space as the 16-cell honeycomb.

Exactly 24 regular octahedral pyramids will fit together around a vertex in four-dimensional space (the apex of each pyramid). This construction yields a 24-cell with octahedral bounding cells, surrounding a central vertex with 24 edge-length long radii. The 4-dimensional content of a unit-edge-length 24-cell is 2, so the content of the regular octahedral pyramid is 1/12. The 24-cell tessellates 4-dimensional space as the 24-cell honeycomb.

The octahedral pyramid is the vertex figure for a truncated 5-orthoplex, .

The graph of the octahedral pyramid is the only possible minimal counterexample to Negami's conjecture, that the connected graphs with planar covers are themselves projective-planar.^[2]

Example 4-dimensional coordinates, 6 points in first 3 coordinates for cube and 4th dimension for the apex. ${\begin{array}{lllr}(\pm 1,&0,&0;&0)\\(0,&\pm 1,&0;&0)\\(0,&0,&\pm 1;&0)\\(0,&0,&0;&\ 1)\end{array}}$

Other polytopes

Cubic pyramid

The dual to the octahedral pyramid is a cubic pyramid, seen as a cubic base and 6 square pyramids meeting at an apex.

Example 4-dimensional coordinates, 8 points in first 3 coordinates for cube and 4th dimension for the apex. ${\begin{array}{lllr}(\pm 1,&\pm 1,&\pm 1;&0)\\(0,&0,&0;&1)\end{array}}$

Square-pyramidal pyramid

The square-pyramidal pyramid, ( ) ∨ [( ) ∨ {4}], is a bisected octahedral pyramid. It has a square pyramid base, and 4 tetrahedrons along with another one more square pyramid meeting at the apex. It can also be seen in an edge-centered projection as a square bipyramid with four tetrahedra wrapped around the common edge. If the height of the two apexes are the same, it can be given a higher symmetry name [( ) ∨ ( )] ∨ {4} = { } ∨ {4}, joining an edge to a perpendicular square.^[3]

The square-pyramidal pyramid can be distorted into a rectangular-pyramidal pyramid, { } ∨ [{ } × { }] or a rhombic-pyramidal pyramid, { } ∨ [{ } + { }], or other lower symmetry forms.

The square-pyramidal pyramid exists as a vertex figure in uniform polytopes of the form , including the bitruncated 5-orthoplex and bitruncated tesseractic honeycomb.

Example 4-dimensional coordinates, 2 coordinates for square, and axial points for pyramidal points. ${\begin{array}{lllr}(\pm 1,&\pm 1;&0;&0)\\(0,&0;&1;&0)\\(0,&0;&0;&\ \ 1)\end{array}}$

Related Research Articles

<span class="mw-page-title-main">Cuboctahedron</span> Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.

In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

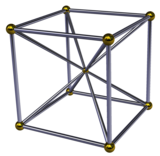
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C₁₆, hexadecachoron, or hexdecahedroid [sic?].

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.

In hyperbolic geometry, the order-4 dodecahedral honeycomb is one of four compact regular space-filling tessellations of hyperbolic 3-space. With Schläfli symbol ${5,3,4},$ it has four dodecahedra around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes. Its dual is the order-5 cubic honeycomb.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.

In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In five-dimensional geometry, a rectified 5-simplex is a convex uniform 5-polytope, being a rectification of the regular 5-simplex.

In eight-dimensional geometry, a rectified 8-orthoplex is a convex uniform 8-polytope, being a rectification of the regular 8-orthoplex.

In five-dimensional geometry, a truncated 5-cube is a convex uniform 5-polytope, being a truncation of the regular 5-cube.

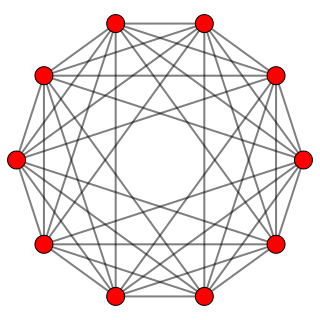
In five-dimensional geometry, a truncated 5-orthoplex is a convex uniform 5-polytope, being a truncation of the regular 5-orthoplex.

In six-dimensional geometry, a truncated 6-cube is a convex uniform 6-polytope, being a truncation of the regular 6-cube.

In 4-dimensional geometry, the cubic pyramid is bounded by one cube on the base and 6 square pyramid cells which meet at the apex. Since a cube has a circumradius divided by edge length less than one, the square pyramids can be made with regular faces by computing the appropriate height.

The order-4 octahedral honeycomb is a regular paracompact honeycomb in hyperbolic 3-space. It is paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {3,4,4}, it has four ideal octahedra around each edge, and infinite octahedra around each vertex in a square tiling vertex figure.

References

↑ Klitzing, Richard. "3D convex uniform polyhedra x3o4o - oct". 1/sqrt(2) = 0.707107
↑ Hliněný, Petr (2010), "20 years of Negami's planar cover conjecture" (PDF), Graphs and Combinatorics , 26 (4): 525–536, CiteSeerX 10.1.1.605.4932 , doi:10.1007/s00373-010-0934-9, MR 2669457, S2CID 121645
↑ Klitzing, Richard. "Segmentotope squasc, K-4.4".

External links

Olshevsky, George. "Pyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
Klitzing, Richard. "4D Segmentotopes".
- Klitzing, Richard. "Segmentotope octpy, K-4.3".
Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra

This 4-polytope article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Klitzing, Richard. "3D convex uniform polyhedra x3o4o - oct". 1/sqrt(2) = 0.707107

[2] Hliněný, Petr (2010), "20 years of Negami's planar cover conjecture" (PDF), Graphs and Combinatorics , 26 (4): 525–536, CiteSeerX 10.1.1.605.4932 , doi:10.1007/s00373-010-0934-9, MR 2669457, S2CID 121645

[3] Klitzing, Richard. "Segmentotope squasc, K-4.4".

[1]

[2]

[3]