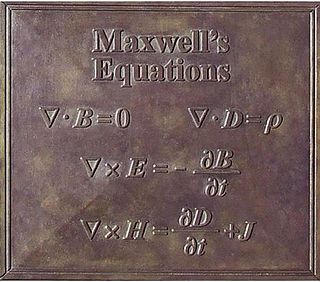In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy.
An electromagnetic field is a physical field, mathematical functions of position and time, representing the influences on and due to electric charges. The field at any point in space and time can be regarded as a combination of an electric field and a magnetic field. Because of the interrelationship between the fields, a disturbance in the electric field can create a disturbance in the magnetic field which in turn affects the electric field, leading to an oscillation that propagates through space, known as an electromagnetic wave.
In physics, specifically in electromagnetism, the Lorentz force law is the combination of electric and magnetic force on a point charge due to electromagnetic fields. The Lorentz force, on the other hand, is a physical effect that occurs in the vicinity of electrically neutral, current-carrying conductors causing moving electrical charges to experience a magnetic force.
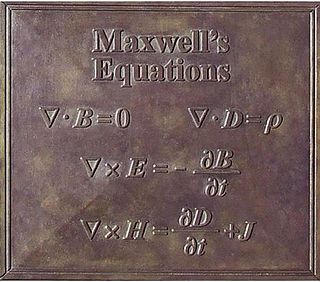
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.
A magnetic field is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.
An electric field is the physical field that surrounds electrically charged particles. Charged particles exert attractive forces on each other when their charges are opposite, and repulse each other when their charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. The electric field of a single charge describes their capacity to exert such forces on another charged object. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Thus, we may informally say that the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker further away. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, Electromagnetism is one of the four fundamental interactions of nature.
Electromagnetic or magnetic induction is the production of an electromotive force (emf) across an electrical conductor in a changing magnetic field.
In physics, specifically electromagnetism, the Biot–Savart law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current.
In classical electromagnetism, Ampère's circuital law relates the circulation of a magnetic field around a closed loop to the electric current passing through the loop.
In electromagnetism, displacement current density is the quantity ∂D/∂t appearing in Maxwell's equations that is defined in terms of the rate of change of D, the electric displacement field. Displacement current density has the same units as electric current density, and it is a source of the magnetic field just as actual current is. However it is not an electric current of moving charges, but a time-varying electric field. In physical materials, there is also a contribution from the slight motion of charges bound in atoms, called dielectric polarization.
A Treatise on Electricity and Magnetism is a two-volume treatise on electromagnetism written by James Clerk Maxwell in 1873. Maxwell was revising the Treatise for a second edition when he died in 1879. The revision was completed by William Davidson Niven for publication in 1881. A third edition was prepared by J. J. Thomson for publication in 1892.
"A Dynamical Theory of the Electromagnetic Field" is a paper by James Clerk Maxwell on electromagnetism, published in 1865. In the paper, Maxwell derives an electromagnetic wave equation with a velocity for light in close agreement with measurements made by experiment, and deduces that light is an electromagnetic wave.
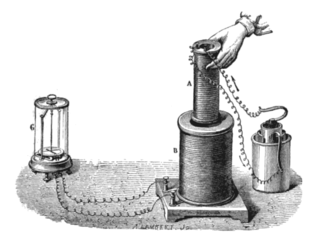
Faraday's law of induction is a law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (emf). This phenomenon, known as electromagnetic induction, is the fundamental operating principle of transformers, inductors, and many types of electric motors, generators and solenoids.
A classical field theory is a physical theory that predicts how one or more fields in physics interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field B, takes the form:
Heaviside–Lorentz units constitute a system of units and quantities that extends the CGS with a particular set of equations that defines electromagnetic quantities, named for Oliver Heaviside and Hendrik Antoon Lorentz. They share with the CGS-Gaussian system that the electric constant ε0 and magnetic constant µ0 do not appear in the defining equations for electromagnetism, having been incorporated implicitly into the electromagnetic quantities. Heaviside–Lorentz units may be thought of as normalizing ε0 = 1 and µ0 = 1, while at the same time revising Maxwell's equations to use the speed of light c instead.
The moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in the frame of reference of the magnet and in the frame of reference of the conductor. The observable quantity in the experiment, the current, is the same in either case, in accordance with the basic principle of relativity, which states: "Only relative motion is observable; there is no absolute standard of rest". However, according to Maxwell's equations, the charges in the conductor experience a magnetic force in the frame of the magnet and an electric force in the frame of the conductor. The same phenomenon would seem to have two different descriptions depending on the frame of reference of the observer.
In physics, Gauss's law for magnetism is one of the four Maxwell's equations that underlie classical electrodynamics. It states that the magnetic field B has divergence equal to zero, in other words, that it is a solenoidal vector field. It is equivalent to the statement that magnetic monopoles do not exist. Rather than "magnetic charges", the basic entity for magnetism is the magnetic dipole.
In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. A weather map, with the surface temperature described by assigning a number to each point on the map, is an example of a scalar field. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.
By the first half of the 19th century, the understanding of electromagnetics had improved through many experiments and theoretical work. In the 1780s, Charles-Augustin de Coulomb established his law of electrostatics. In 1825, André-Marie Ampère published his force law. In 1831, Michael Faraday discovered electromagnetic induction through his experiments, and proposed lines of forces to describe it. In 1834, Emil Lenz solved the problem of the direction of the induction, and Franz Ernst Neumann wrote down the equation to calculate the induced force by change of magnetic flux. However, these experimental results and rules were not well organized and sometimes confusing to scientists. A comprehensive summary of the electrodynamic principles was needed.
