
Diatomic molecules are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen or oxygen, then it is said to be homonuclear. Otherwise, if a diatomic molecule consists of two different atoms, such as carbon monoxide or nitric oxide, the molecule is said to be heteronuclear. The bond in a homonuclear diatomic molecule is non-polar.

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense fervent in the development of quantum mechanics.
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for every locally finite partially ordered set and commutative ring with unity. Subalgebras called reduced incidence algebras give a natural construction of various types of generating functions used in combinatorics and number theory.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
Rotational–vibrational spectroscopy is a branch of molecular spectroscopy that is concerned with infrared and Raman spectra of molecules in the gas phase. Transitions involving changes in both vibrational and rotational states can be abbreviated as rovibrational transitions. When such transitions emit or absorb photons, the frequency is proportional to the difference in energy levels and can be detected by certain kinds of spectroscopy. Since changes in rotational energy levels are typically much smaller than changes in vibrational energy levels, changes in rotational state are said to give fine structure to the vibrational spectrum. For a given vibrational transition, the same theoretical treatment as for pure rotational spectroscopy gives the rotational quantum numbers, energy levels, and selection rules. In linear and spherical top molecules, rotational lines are found as simple progressions at both higher and lower frequencies relative to the pure vibration frequency. In symmetric top molecules the transitions are classified as parallel when the dipole moment change is parallel to the principal axis of rotation, and perpendicular when the change is perpendicular to that axis. The ro-vibrational spectrum of the asymmetric rotor water is important because of the presence of water vapor in the atmosphere.

Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The rotational spectrum of polar molecules can be measured in absorption or emission by microwave spectroscopy or by far infrared spectroscopy. The rotational spectra of non-polar molecules cannot be observed by those methods, but can be observed and measured by Raman spectroscopy. Rotational spectroscopy is sometimes referred to as pure rotational spectroscopy to distinguish it from rotational-vibrational spectroscopy where changes in rotational energy occur together with changes in vibrational energy, and also from ro-vibronic spectroscopy where rotational, vibrational and electronic energy changes occur simultaneously.

Molecular hydrogen occurs in two isomeric forms, one with its two proton nuclear spins aligned parallel (orthohydrogen), the other with its two proton spins aligned antiparallel (parahydrogen). These two forms are often referred to as spin isomers or as nuclear spin isomers.
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.

In mathematics and especially in combinatorics, a plane partition is a two-dimensional array of nonnegative integers that is nonincreasing in both indices. This means that

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. Although Routhian mechanics is equivalent to Lagrangian mechanics and Hamiltonian mechanics, and introduces no new physics, it offers an alternative way to solve mechanical problems.
The vibrational partition function traditionally refers to the component of the canonical partition function resulting from the vibrational degrees of freedom of a system. The vibrational partition function is only well-defined in model systems where the vibrational motion is relatively uncoupled with the system's other degrees of freedom.
In mathematics, the multiple zeta functions are generalizations of the Riemann zeta function, defined by
In the mathematical field of linear algebra, an arrowhead matrix is a square matrix containing zeros in all entries except for the first row, first column, and main diagonal, these entries can be any number. In other words, the matrix has the form

The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure; i.e., at these conditions the adsorbate's partial pressure is related to its volume V adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule and an empty sorption site S. This reaction yields an adsorbed species with an associated equilibrium constant :
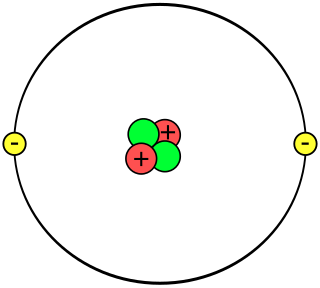
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.

In complex analysis and geometric function theory, the Grunsky matrices, or Grunsky operators, are infinite matrices introduced in 1939 by Helmut Grunsky. The matrices correspond to either a single holomorphic function on the unit disk or a pair of holomorphic functions on the unit disk and its complement. The Grunsky inequalities express boundedness properties of these matrices, which in general are contraction operators or in important special cases unitary operators. As Grunsky showed, these inequalities hold if and only if the holomorphic function is univalent. The inequalities are equivalent to the inequalities of Goluzin, discovered in 1947. Roughly speaking, the Grunsky inequalities give information on the coefficients of the logarithm of a univalent function; later generalizations by Milin, starting from the Lebedev–Milin inequality, succeeded in exponentiating the inequalities to obtain inequalities for the coefficients of the univalent function itself. The Grunsky matrix and its associated inequalities were originally formulated in a more general setting of univalent functions between a region bounded by finitely many sufficiently smooth Jordan curves and its complement: the results of Grunsky, Goluzin and Milin generalize to that case.
In fluid dynamics, Beltrami flows are flows in which the vorticity vector and the velocity vector are parallel to each other. In other words, Beltrami flow is a flow in which the Lamb vector is zero. It is named after the Italian mathematician Eugenio Beltrami due to his derivation of the Beltrami vector field, while initial developments in fluid dynamics were done by the Russian scientist Ippolit S. Gromeka in 1881.
In number theory, the prime omega functions and count the number of prime factors of a natural number Thereby counts each distinct prime factor, whereas the related function counts the total number of prime factors of honoring their multiplicity. That is, if we have a prime factorization of of the form for distinct primes , then the respective prime omega functions are given by and . These prime factor counting functions have many important number theoretic relations.




















































