
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models.

Ferromagnetism is a property of certain materials that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are familiar metals that are noticeably attracted to a magnet, a consequence of their substantial magnetic permeability. Magnetic permeability describes the induced magnetization of a material due to the presence of an external magnetic field. This temporarily induced magnetization, for example, inside a steel plate, accounts for its attraction to the permanent magnet. Whether or not that steel plate acquires a permanent magnetization itself depends not only on the strength of the applied field but on the so-called coercivity of the ferromagnetic material, which can vary greatly.

Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, magnetism is one of two aspects of electromagnetism.

A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.
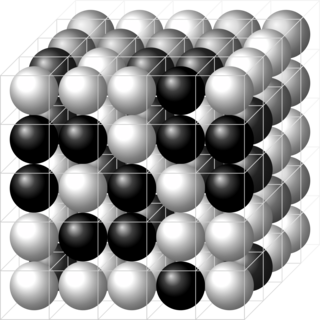
In mathematical physics, a lattice model is a mathematical model of a physical system that is defined on a lattice, as opposed to a continuum, such as the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are quite popular in theoretical physics, for many reasons. Some models are exactly solvable, and thus offer insight into physics beyond what can be learned from perturbation theory. Lattice models are also ideal for study by the methods of computational physics, as the discretization of any continuum model automatically turns it into a lattice model. The exact solution to many of these models includes the presence of solitons. Techniques for solving these include the inverse scattering transform and the method of Lax pairs, the Yang–Baxter equation and quantum groups. The solution of these models has given insights into the nature of phase transitions, magnetization and scaling behaviour, as well as insights into the nature of quantum field theory. Physical lattice models frequently occur as an approximation to a continuum theory, either to give an ultraviolet cutoff to the theory to prevent divergences or to perform numerical computations. An example of a continuum theory that is widely studied by lattice models is the QCD lattice model, a discretization of quantum chromodynamics. However, digital physics considers nature fundamentally discrete at the Planck scale, which imposes upper limit to the density of information, aka Holographic principle. More generally, lattice gauge theory and lattice field theory are areas of study. Lattice models are also used to simulate the structure and dynamics of polymers.

In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. The magnetic moment is typically expressed as a vector. Examples of objects that have magnetic moments include loops of electric current, permanent magnets, elementary particles, composite particles, various molecules, and many astronomical objects.
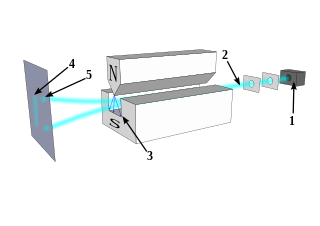
In quantum physics, the Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially-varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment were deflected, owing to the magnetic field gradient, from a straight path. The screen revealed discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.
In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment is −9.2847647043(28)×10−24 J⋅T−1. In units of the Bohr magneton (μB), it is −1.00115965218059(13) μB, a value that was measured with a relative accuracy of 1.3×10−13.
The Classical Heisenberg model, developed by Werner Heisenberg, is the case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.

A spin ice is a magnetic substance that does not have a single minimal-energy state. It has magnetic moments (i.e. "spin") as elementary degrees of freedom which are subject to frustrated interactions. By their nature, these interactions prevent the moments from exhibiting a periodic pattern in their orientation down to a temperature much below the energy scale set by the said interactions. Spin ices show low-temperature properties, residual entropy in particular, closely related to those of common crystalline water ice. The most prominent compounds with such properties are dysprosium titanate (Dy2Ti2O7) and holmium titanate (Ho2Ti2O7). The orientation of the magnetic moments in spin ice resembles the positional organization of hydrogen atoms (more accurately, ionized hydrogen, or protons) in conventional water ice (see figure 1).
In chemistry and physics, the exchange interaction or exchange splitting is a quantum mechanical effect that only occurs between identical particles. Despite sometimes being called an exchange force in an analogy to classical force, it is not a true force as it lacks a force carrier.
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction.

Alexander Leonidovich Kuzemsky is a Russian theoretical physicist.
In quantum physics, the quantum inverse scattering method (QISM) or the algebraic Bethe ansatz is a method for solving integrable models in 1+1 dimensions, introduced by Leon Takhtajan and L. D. Faddeev in 1979.
The quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotors that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments. The model differs from similar spin-models such as the Ising model and the Heisenberg model in that it includes a term analogous to kinetic energy.
Exact diagonalization (ED) is a numerical technique used in physics to determine the eigenstates and energy eigenvalues of a quantum Hamiltonian. In this technique, a Hamiltonian for a discrete, finite system is expressed in matrix form and diagonalized using a computer. Exact diagonalization is only feasible for systems with a few tens of particles, due to the exponential growth of the Hilbert space dimension with the size of the quantum system. It is frequently employed to study lattice models, including the Hubbard model, Ising model, Heisenberg model, t-J model, and SYK model.
Magnetic 2D materials or magnetic van der Waals materials are two-dimensional materials that display ordered magnetic properties such as antiferromagnetism or ferromagnetism. After the discovery of graphene in 2004, the family of 2D materials has grown rapidly. There have since been reports of several related materials, all except for magnetic materials. But since 2016 there have been numerous reports of 2D magnetic materials that can be exfoliated with ease just like graphene.
The nucleon magnetic moments are the intrinsic magnetic dipole moments of the proton and neutron, symbols μp and μn. The nucleus of an atom comprises protons and neutrons, both nucleons that behave as small magnets. Their magnetic strengths are measured by their magnetic moments. The nucleons interact with normal matter through either the nuclear force or their magnetic moments, with the charged proton also interacting by the Coulomb force.
A spin chain is a type of model in statistical physics. Spin chains were originally formulated to model magnetic systems, which typically consist of particles with magnetic spin located at fixed sites on a lattice. A prototypical example is the quantum Heisenberg model. Interactions between the sites are modelled by operators which act on two different sites, often neighboring sites.









