An equal temperament is a musical temperament, or a system of tuning, in which the frequency interval between every pair of adjacent notes has the same ratio. In other words, the ratios of the frequencies of any adjacent pair of notes is the same, and, as pitch is perceived roughly as the logarithm of frequency, equal perceived "distance" from every note to its nearest neighbor.

In music, just intonation or pure intonation is the tuning of musical intervals as (small) whole number ratios of frequencies. Any interval tuned in this way is called a just interval. Just intervals and chords are aggregates of harmonic series partials and may be seen as sharing a (lower) implied fundamental. For example, a tone with a frequency of 300 Hz and another with a frequency of 200 Hz are both multiples of 100 Hz. Their interval is, therefore, an aggregate of the second and third partials of the harmonic series of an implied fundamental frequency 100 Hz.
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale. Some scales contain different pitches when ascending than when descending, for example, the melodic minor scale.

In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.

The Bohlen–Pierce scale is a musical tuning and scale, first described in the 1970s, that offers an alternative to the octave-repeating scales typical in Western and other musics, specifically the equal tempered diatonic scale.

In music theory, a minor chord is a chord having a root, a minor third, and a perfect fifth. When a chord has these three notes alone, it is called a minor triad. Some minor triads with additional notes, such as the minor seventh chord, may also be called minor chords.

An augmented triad is a chord, made up of two major thirds. The term augmented triad arises from an augmented triad being considered a major chord whose top note (fifth) is raised. It is indicated by the symbol "+" or "aug", and can be represented by the integer notation {0, 4, 8}.
In music, a triad is a set of three notes that can be stacked vertically in thirds. The term "harmonic triad" was coined by Johannes Lippius in his Synopsis musicae novae (1612).
Coltrane changes are a harmonic progression variation using substitute chords over common jazz chord progressions. These substitution patterns were first demonstrated by jazz musician John Coltrane on the albums Bags & Trane and Cannonball Adderley Quintet in Chicago. Coltrane continued his explorations on the 1960 album Giant Steps and expanded on the substitution cycle in his compositions "Giant Steps" and "Countdown", the latter of which is a reharmonized version of Eddie Vinson's "Tune Up". The Coltrane changes are a standard advanced harmonic substitution used in jazz improvisation.
In Western music, the adjectives major and minor can describe a musical composition, movement, section, scale, key, chord, or interval.
The twelfth root of two or is an algebraic irrational number. It is most important in Western music theory, where it represents the frequency ratio of a semitone in twelve-tone equal temperament. This number was proposed for the first time in relationship to musical tuning in the sixteenth and seventeenth centuries. It allows measurement and comparison of different intervals as consisting of different numbers of a single interval, the equal tempered semitone. A semitone itself is divided into 100 cents.

In music, the septimal minor thirdplay (help·info), also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5. In 24-tone equal temperament five quarter tones approximate the septimal minor third at 250 cents.

A neutral third is a musical interval wider than a minor third play (help·info) but narrower than a major third play (help·info), named by Jan Pieter Land in 1880. Land makes reference to the neutral third attributed to Zalzal, described by Al-Farabi as corresponing to a ratio of 27:22 and by Avicenna as 39:32. The Zalzalian third may have been a mobile interval.

The Harmonic Table note-layout, or tonal array, is a key layout for musical instruments that offers interesting advantages over the traditional keyboard layout.

The α (alpha) scale is a non-octave-repeating musical scale invented by Wendy Carlos and first used on her album Beauty in the Beast (1986). It is derived from approximating just intervals using multiples of a single interval without, as is standard in equal temperaments, requiring an octave (2:1). It may be approximated by dividing the perfect fifth (3:2) into nine equal steps, or by dividing the minor third (6:5) into four steps.

The β (beta) scale is a non-octave-repeating musical scale invented by Wendy Carlos and first used on her album Beauty in the Beast (1986). It is derived from approximating just intervals using multiples of a single interval without, as is standard in equal temperaments, requiring an octave (2:1). It may be approximated by splitting the perfect fifth (3:2) into eleven equal parts. It may be approximated by splitting the perfect fourth (4:3) into two equal parts, or eight equal parts ( ), totaling approximately 18.8 steps per octave.

The γ (gamma) scale is a non-octave repeating musical scale invented by Wendy Carlos while preparing Beauty in the Beast (1986) though it is does not appear on the album. It is derived from approximating just intervals using multiples of a single interval without, as is standard in equal temperaments, requiring an octave (2:1). It may be approximated by splitting the perfect fifth (3:2) into 20 equal parts, by splitting the neutral third into two equal parts, or ten equal parts of approximately 35.1 cents each for 34.188 steps per octave.

The δ (delta) scale is a non-octave repeating musical scale. It may be regarded as the beta scale's reciprocal since it is, "as far 'down' the circle from α as β is 'up.'" As such it would split the minor second into eight equal parts of approximately 14 cents each Play (help·info). This would total approximately 85.7 steps per octave.
Heinz P. Bohlen was a microwave electronics and communications engineer.

The 833 cents scale is a musical tuning and scale proposed by Heinz Bohlen based on combination tones, an interval of 833.09 cents, and, coincidentally, the Fibonacci sequence. The golden ratio is 1.6180339..., which as a musical interval is 833.09 cents. In the 833 cents scale this interval is taken as an alternative to the octave as the interval of repetition, however the golden ratio is not regarded as an equivalent interval. Other music theorists such as Walter O'Connell, in his "The Tonality of the Golden Section", and Loren Temes appear to have also created this scale prior to Bohlen's discovery of it.

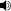

![]()
![]()