
A harmonic series is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency.

In music, just intonation or pure intonation is the attempt to tune all musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and may be called a just interval; when it is sounded, no beating is heard. Just intervals consist of members of a single harmonic series of an implied fundamental. For example, in the diagram, the notes G3 and C4 may be tuned as members of the harmonic series of the lowest C, in which case their frequencies will be 3 and 4 times, respectively, the fundamental frequency and their interval ratio equal to 4:3; they may also be tuned differently.

In music, there are two common meanings for tuning:
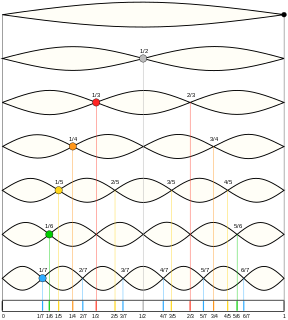
A harmonic is a wave with a frequency that is a positive integer multiple of the fundamental frequency, the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the 1st harmonic, the other harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a harmonic series.
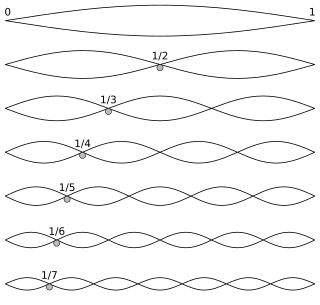
An overtone is any harmonic with frequency greater than the fundamental frequency of a sound. In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound.

Harry Partch was an American composer, music theorist, and creator of musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century composers in the West to work systematically with microtonal scales. He built custom-made instruments in these tunings on which to play his compositions, and described his theory and practice in his book Genesis of a Music (1947).

In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term limit was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name.

Xenharmonic music is that which uses a tuning system which neither conforms to nor closely approximates the common 12-tone equal temperament. The term xenharmonic was coined by Ivor Darreg, from xenia, "hospitable," and xenos "foreign." He stated it as being "intended to include just intonation and such temperaments as the 5-, 7-, and 11-tone, along with the higher-numbered really-microtonal systems as far as one wishes to go."

In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions. The minor third is one of two commonly occurring thirds. It is called minor because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones. The minor third is a skip melodically.

A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, and have 24 different pitches.
Musical acoustics or music acoustics is a multidisciplinary field that combines knowledge from physics, psychophysics, organology(classification of the instruments), physiology, music theory, ethnomusicology, signal processing and instrument building, among other disciplines. As a branch of acoustics, it is concerned with researching and describing the physics of music – how sounds are employed to make music. Examples of areas of study are the function of musical instruments, the human voice, computer analysis of melody, and in the clinical use of music in music therapy.

The 43-tone scale is a just intonation scale with 43 pitches in each octave. It is based on an eleven-limit tonality diamond, similar to the seven-limit diamond previously devised by Max Friedrich Meyer and refined by Harry Partch.

Otonality and utonality are terms introduced by Harry Partch to describe chords whose pitch classes are the harmonics or subharmonics of a given fixed tone (identity), respectively. For example: 1/1, 2/1, 3/1,... or 1/1, 1/2, 1/3,....
An Otonality is that set of pitches generated by the numerical factors (...identities)...over a numerical constant in the denominator. Conversely, a Utonality is the inversion of an Otonality, a set of pitches with a numerical constant in the numerator over the numerical factors...in the denominator.
In music, intonation is the pitch accuracy of a musician or musical instrument. Intonation may be flat, sharp, or both, successively or simultaneously.

In music, the septimal minor third, also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5. In 24-tone equal temperament five quarter tones approximate the septimal minor third at 250 cents. A septimal minor third is almost exactly two-ninths of an octave, and thus all divisions of the octave into multiples of nine have an almost perfect match to this interval. The septimal major sixth, 12/7, is the inverse of this interval.
In music, the undertone series or subharmonic series is a sequence of notes that results from inverting the intervals of the overtone series. While overtones naturally occur with the physical production of music on instruments, undertones must be produced in unusual ways. While the overtone series is based upon arithmetic multiplication of frequencies, resulting in a harmonic series, the undertone series is based on arithmetic division.

Playing a string harmonic is a string instrument technique that uses the nodes of natural harmonics of a musical string to isolate overtones. Playing string harmonics produces high pitched tones, often compared in timbre to a whistle or flute. Overtones can be isolated "by lightly touching the string with the finger instead of pressing it down" against the fingerboard.

The Moodswinger is a twelve-string electric zither with an additional third bridge designed by Yuri Landman. The rod which functions as the third bridge divides the strings into two sections to cause an overtone multiphonic sound. One of the copies of the instrument is part of the collection of the Musical Instrument Museum in Phoenix, Arizona.

Genesis of a Music is a book first published in 1949 by microtonal composer Harry Partch (1901–1974).

The 3rd bridge is an extended playing technique used on the electric guitar and other string instruments that allows a musician to produce distinctive timbres and overtones that are unavailable on a conventional string instrument with two bridges. The timbre created with this technique is close to that of gamelan instruments like the bonang and similar Indonesian types of pitched gongs.
A third bridge can be devised by inserting a rigid preparation object between the strings and the body or neck of the instrument, effectively diving the string into distinct vibrating segments.



 Play (help·info)
Play (help·info)

















