An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, which gives an equal perceived step size as pitch is perceived roughly as the logarithm of frequency.
In music, just intonation or pure intonation is the attempt to tune all musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and may be called a just interval; when it is sounded, no beating is heard. Just intervals consist of members of a single harmonic series of an implied fundamental. For example, in the diagram, the notes G3 and C4 may be tuned as members of the harmonic series of the lowest C, in which case their frequencies will be 3 and 4 times, respectively, the fundamental frequency and their interval ratio equal to 4:3; they may also be tuned differently.
In music, there are two common meanings for tuning:
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80. Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the Pythagorean major third to a just major third.
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals produced by other tuning systems, including most meantone temperaments.
The Bohlen–Pierce scale is a musical tuning and scale, first described in the 1970s, that offers an alternative to the octave-repeating scales typical in Western and other musics, specifically the equal-tempered diatonic scale.
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.
A schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament, Helmholtz temperament, or quasi-Pythagorean temperament.
The twelfth root of two or is an algebraic irrational number, approximately equal to 1.06. It is most important in Western music theory, where it represents the frequency ratio of a semitone in twelve-tone equal temperament. This number was proposed for the first time in relationship to musical tuning in the sixteenth and seventeenth centuries. It allows measurement and comparison of different intervals as consisting of different numbers of a single interval, the equal tempered semitone. A semitone itself is divided into 100 cents.
In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
Quarter-comma meantone, or 1⁄4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81:80), with respect to its just intonation used in Pythagorean tuning ; the result is 3/2 × 1⁄4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.
In music, 72 equal temperament, called twelfth-tone, 72-TET, 72-EDO, or 72-ET, is the tempered scale derived by dividing the octave into twelfth-tones, or in other words 72 equal steps. Play (help·info) Each step represents a frequency ratio of 72√2, or 16+2⁄3 cents, which divides the 100 cent "halftone" into 6 equal parts and is thus a "twelfth-tone". Since 72 is divisible by 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72, 72-EDO includes all those equal temperaments. Since it contains so many temperaments, 72-EDO contains at the same time tempered semitones, third-tones, quartertones and sixth-tones, which makes it a very versatile temperament.
Twelve-tone equal temperament is the musical system that divides the octave into 12 parts, all of which are equally tempered on a logarithmic scale, with a ratio equal to the 12th root of 2. That resulting smallest interval, 1⁄12 the width of an octave, is called a semitone or half step.
In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Play (help·info) Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET or 31-EDO, also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps. Play (help·info) Each step represents a frequency ratio of 31√2, or 38.71 cents.
In music, 19 equal temperament, called 19 TET, 19 EDO, or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps. Each step represents a frequency ratio of 19√2, or 63.16 cents.
In musical theory, 34 equal temperament, also referred to as 34-TET, 34-EDO or 34-ET, is the tempered tuning derived by dividing the octave into 34 equal-sized steps. Play (help·info) Each step represents a frequency ratio of 34√2, or 35.29 cents Play (help·info).
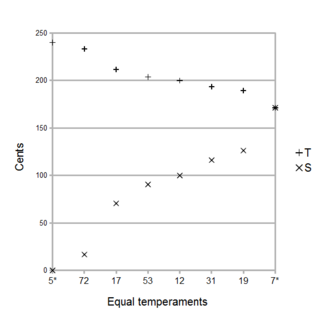
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.
In music theory, a neutral interval is an interval that is neither a major nor minor, but instead in between. For example, in equal temperament, a major third is 400 cents, a minor third is 300 cents, and a neutral third is 350 cents. A neutral interval inverts to a neutral interval. For example, the inverse of a neutral third is a neutral sixth.
Play (help·info))), so that five of them add up to an approximate 3/1 (an octave plus a perfect fifth). A chain of these thirds can be used to generate a 7-tone scale with the following interval distribution (given in cents):