An equal temperament is a musical temperament or tuning system that approximates just intervals but instead divides an octave into steps such that the ratio of the frequencies of any adjacent pair of notes is the same. This system yields pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in turn are important in cryptography.

In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term limit was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

In mathematics, a superparticular ratio, also called a superparticular number or epimoric ratio, is the ratio of two consecutive integer numbers.
In Western music, the adjectives major and minor may describe an interval, chord, scale, or key. A composition, movement, section, or phrase may also be referred to by its key, including whether that key is major or minor.

In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.

A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A common, vulgar, or simple fraction consists of an integer numerator, displayed above a line, and a non-zero integer denominator, displayed below that line. If these integers are positive, then the numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. For example, in the fraction 3/4, the numerator 3 indicates that the fraction represents 3 equal parts, and the denominator 4 indicates that 4 parts make up a whole. The picture to the right illustrates 3/4 of a cake.

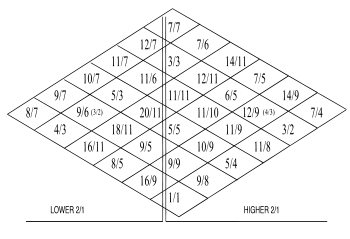
The 43-tone scale is a just intonation scale with 43 pitches in each octave. It is based on an eleven-limit tonality diamond, similar to the seven-limit diamond previously devised by Max Friedrich Meyer and refined by Harry Partch.

Otonality and utonality are terms introduced by Harry Partch to describe chords whose pitch classes are the harmonics or subharmonics of a given fixed tone (identity), respectively. For example: 1/1, 2/1, 3/1,... or 1/1, 1/2, 1/3,....
An Otonality is that set of pitches generated by the numerical factors (...identities)...over a numerical constant in the denominator. Conversely, a Utonality is the inversion of an Otonality, a set of pitches with a numerical constant in the numerator over the numerical factors...in the denominator.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.
In music, septimal meantone temperament, also called standard septimal meantone or simply septimal meantone, refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Meantone temperament represents a frequency ratio of approximately 5 by means of four fifths, so that the major third, for instance C–E, is obtained from two tones in succession. Septimal meantone represents the frequency ratio of 56 (7 × 23) by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C–A♯, not C–B♭, represents a 7:4 interval in septimal meantone.
In music, the undertone series or subharmonic series is a sequence of notes that results from inverting the intervals of the overtone series. While overtones naturally occur with the physical production of music on instruments, undertones must be produced in unusual ways. While the overtone series is based upon arithmetic multiplication of frequencies, resulting in a harmonic series, the undertone series is based on arithmetic division.
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of distinct unit fractions, such as 5/6 = 1/2 + 1/3. As the name indicates, these representations have been used as long ago as ancient Egypt, but the first published systematic method for constructing such expansions was described in 1202 in the Liber Abaci of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction that can be used in any representation of the remaining fraction.

Genesis of a Music is a book first published in 1949 by microtonal composer Harry Partch (1901–1974).
In elementary algebra, root rationalisation is a process by which radicals in the denominator of an algebraic fraction are eliminated.
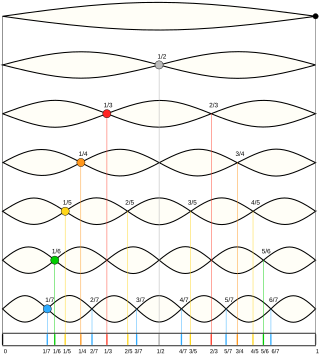
The scale of harmonics is a musical scale based on the noded positions of the natural harmonics existing on a string. This musical scale is present on the guqin, regarded as one of the first string instruments with a musical scale. Most fret positions appearing on Non-Western string instruments (lutes) are equal to positions of this scale. Unexpectedly, these fret positions are actually the corresponding undertones of the overtones from the harmonic series. The distance from the nut to the fret is an integer number lower than the distance from the fret to the bridge.

The American composer Harry Partch (1901-1974) composed using scales of unequal intervals in just intonation, derived from the natural Harmonic series; these scales allowed for more tones of smaller intervals than in the standard Western tuning, which uses twelve equal intervals. The tonal system Partch used has 43 tones to the octave. To play this music he invented and built many new instruments, with names such as the Chromelodeon, the Quadrangularis Reversum, and the Zymo-Xyl.