
An equal temperament is a musical temperament or tuning system that approximates just intervals but instead divides an octave into steps such that the ratio of the frequencies of any adjacent pair of notes is the same. This system yields pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency.

In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

In music, there are two common meanings for tuning:

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written note, interval, or chord is an alternative way to write that note, interval, or chord. The term is derived from Latin enharmonicus, from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος (enarmónios), from ἐν (en) and ἁρμονία (harmonía).

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, and have 24 different pitches.

Scientific pitch notation (SPN), also known as American standard pitch notation (ASPN) and international pitch notation (IPN), is a method of specifying musical pitch by combining a musical note name and a number identifying the pitch's octave.
The twelfth root of two or is an algebraic irrational number, approximately equal to 1.0594631. It is most important in Western music theory, where it represents the frequency ratio of a semitone in twelve-tone equal temperament. This number was proposed for the first time in relationship to musical tuning in the sixteenth and seventeenth centuries. It allows measurement and comparison of different intervals as consisting of different numbers of a single interval, the equal tempered semitone. A semitone itself is divided into 100 cents.

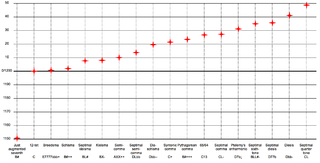
In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
In music, 72 equal temperament, called twelfth-tone, 72-TET, 72-EDO, or 72-ET, is the tempered scale derived by dividing the octave into twelfth-tones, or in other words 72 equal steps. Each step represents a frequency ratio of 72√2, or 16+2⁄3 cents, which divides the 100 cent "halftone" into 6 equal parts and is thus a "twelfth-tone". Since 72 is divisible by 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72, 72-EDO includes all those equal temperaments. Since it contains so many temperaments, 72-EDO contains at the same time tempered semitones, third-tones, quartertones and sixth-tones, which makes it a very versatile temperament.
12 equal temperament (12-ET) is the musical system that divides the octave into 12 parts, all of which are equally tempered on a logarithmic scale, with a ratio equal to the 12th root of 2. That resulting smallest interval, 1⁄12 the width of an octave, is called a semitone or half step.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.

In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET or 31-EDO, also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps. Each step represents a frequency ratio of 31√2, or 38.71 cents.

In music, 19 Tone Equal Temperament, called 19 TET, 19 EDO, 19-ED2 or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps. Each step represents a frequency ratio of 19√2, or 63.16 cents.
In music, 22 equal temperament, called 22-TET, 22-EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps. Each step represents a frequency ratio of 22√2, or 54.55 cents.

Music theory analyzes the pitch, timing, and structure of music. It uses mathematics to study elements of music such as tempo, chord progression, form, and meter. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory.
In music, 41 equal temperament, abbreviated 41-TET, 41-EDO, or 41-ET, is the tempered scale derived by dividing the octave into 41 equally sized steps. Each step represents a frequency ratio of 21/41, or 29.27 cents, an interval close in size to the septimal comma. 41-ET can be seen as a tuning of the schismatic, magic and miracle temperaments. It is the second smallest equal temperament, after 29-ET, whose perfect fifth is closer to just intonation than that of 12-ET. In other words, is a better approximation to the ratio than either or .
In music, 23 equal temperament, called 23-TET, 23-EDO, or 23-ET, is the tempered scale derived by dividing the octave into 23 equal steps. Each step represents a frequency ratio of 23√2, or 52.174 cents. This system is the largest EDO that has an error of at least 20 cents for the 3rd (3:2), 5th (5:4), 7th (7:4), and 11th (11:8) harmonics. The lack of approximation to simple intervals makes the scale notable among those seeking to break free from conventional harmony rules.











