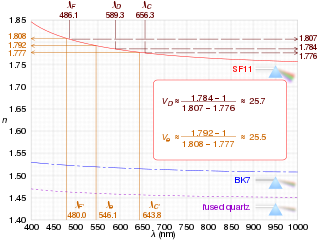
In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion, with high values of V indicating low dispersion. It is named after Ernst Abbe (1840–1905), the German physicist who defined it. The term V-number should not be confused with the normalized frequency in fibers.

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
In physics, coherence length is the propagation distance over which a coherent wave maintains a specified degree of coherence. Wave interference is strong when the paths taken by all of the interfering waves differ by less than the coherence length. A wave with a longer coherence length is closer to a perfect sinusoidal wave. Coherence length is important in holography and telecommunications engineering.
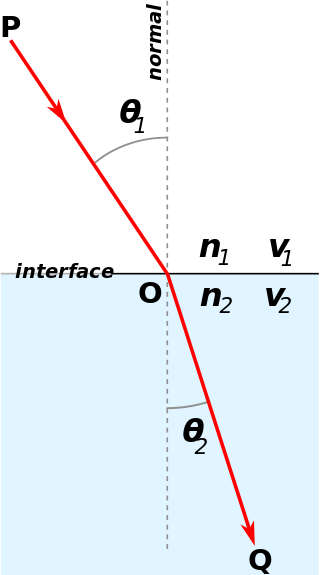
Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.

Magnetic circular dichroism (MCD) is the differential absorption of left and right circularly polarized (LCP and RCP) light, induced in a sample by a strong magnetic field oriented parallel to the direction of light propagation. MCD measurements can detect transitions which are too weak to be seen in conventional optical absorption spectra, and it can be used to distinguish between overlapping transitions. Paramagnetic systems are common analytes, as their near-degenerate magnetic sublevels provide strong MCD intensity that varies with both field strength and sample temperature. The MCD signal also provides insight into the symmetry of the electronic levels of the studied systems, such as metal ion sites.
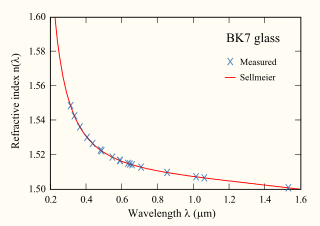
The Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.
Ray transfer matrix analysis is a mathematical form for performing ray tracing calculations in sufficiently simple problems which can be solved considering only paraxial rays. Each optical element is described by a 2×2 ray transfer matrix which operates on a vector describing an incoming light ray to calculate the outgoing ray. Multiplication of the successive matrices thus yields a concise ray transfer matrix describing the entire optical system. The same mathematics is also used in accelerator physics to track particles through the magnet installations of a particle accelerator, see electron optics.

In optics and in wave propagation in general, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular. A medium having this common property may be termed a dispersive medium.

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.
The laser diode rate equations model the electrical and optical performance of a laser diode. This system of ordinary differential equations relates the number or density of photons and charge carriers (electrons) in the device to the injection current and to device and material parameters such as carrier lifetime, photon lifetime, and the optical gain.

Fused quartz,fused silica or quartz glass is a glass consisting of almost pure silica (silicon dioxide, SiO2) in amorphous (non-crystalline) form. This differs from all other commercial glasses in which other ingredients are added which change the glasses' optical and physical properties, such as lowering the melt temperature. Fused quartz, therefore, has high working and melting temperatures, making it less desirable for most common applications.

A zone plate is a device used to focus light or other things exhibiting wave character. Unlike lenses or curved mirrors, zone plates use diffraction instead of refraction or reflection. Based on analysis by French physicist Augustin-Jean Fresnel, they are sometimes called Fresnel zone plates in his honor. The zone plate's focusing ability is an extension of the Arago spot phenomenon caused by diffraction from an opaque disc.
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid. For the case of a finite-dimensional graph, the discrete Laplace operator is more commonly called the Laplacian matrix.
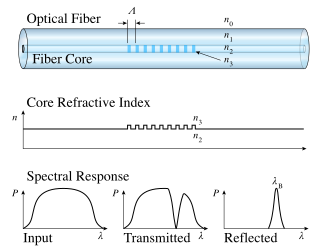
A fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by creating a periodic variation in the refractive index of the fiber core, which generates a wavelength-specific dielectric mirror. Hence a fiber Bragg grating can be used as an inline optical fiber to block certain wavelengths, can be used for sensing applications, or it can be used as wavelength-specific reflector.

In optics, a thin lens is a lens with a thickness that is negligible compared to the radii of curvature of the lens surfaces. Lenses whose thickness is not negligible are sometimes called thick lenses.
Time-domain thermoreflectance is a method by which the thermal properties of a material can be measured, most importantly thermal conductivity. This method can be applied most notably to thin film materials, which have properties that vary greatly when compared to the same materials in bulk. The idea behind this technique is that once a material is heated up, the change in the reflectance of the surface can be utilized to derive the thermal properties. The reflectivity is measured with respect to time, and the data received can be matched to a model with coefficients that correspond to thermal properties.
Quantum mechanics was first applied to optics, and interference in particular, by Paul Dirac. Richard Feynman, in his Lectures on Physics, uses Dirac's notation to describe thought experiments on double-slit interference of electrons. Feynman's approach was extended to N-slit interferometers for either single-photon illumination, or narrow-linewidth laser illumination, that is, illumination by indistinguishable photons, by Frank Duarte. The N-slit interferometer was first applied in the generation and measurement of complex interference patterns.