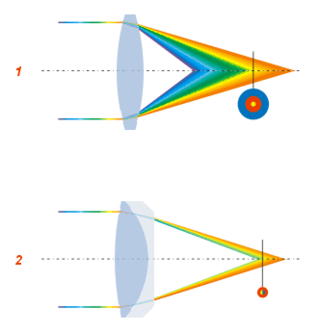
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements.

Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.

A corrective lens is a transmissive optical device that is worn on the eye to improve visual perception. The most common use is to treat refractive errors: myopia, hypermetropia, astigmatism, and presbyopia. Glasses or "spectacles" are worn on the face a short distance in front of the eye. Contact lenses are worn directly on the surface of the eye. Intraocular lenses are surgically implanted most commonly after cataract removal but can be used for purely refractive purposes.

An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths into focus on the same plane. Wavelengths in between these two then have better focus error than could be obtained with a simple lens.

An optical prism is a transparent optical element with flat, polished surfaces that are designed to refract light. At least one surface must be angled — elements with two parallel surfaces are not prisms. The most familiar type of optical prism is the triangular prism, which has a triangular base and rectangular sides. Not all optical prisms are geometric prisms, and not all geometric prisms would count as an optical prism. Prisms can be made from any material that is transparent to the wavelengths for which they are designed. Typical materials include glass, acrylic and fluorite.

Fused quartz, fused silica or quartz glass is a glass consisting of almost pure silica (silicon dioxide, SiO2) in amorphous (non-crystalline) form. This differs from all other commercial glasses, such as soda-lime glass, lead glass, or borosilicate glass, in which other ingredients are added which change the glasses' optical and physical properties, such as lowering the melt temperature, the spectral transmission range, or the mechanical strength. Fused quartz, therefore, has high working and melting temperatures, making it difficult to form and less desirable for most common applications, but is much stronger, more chemically resistant, and exhibits lower thermal expansion, making it more suitable for many specialized uses such as lighting and scientific applications.

An antireflective, antiglare or anti-reflection (AR) coating is a type of optical coating applied to the surface of lenses, other optical elements, and photovoltaic cells to reduce reflection. In typical imaging systems, this improves the efficiency since less light is lost due to reflection. In complex systems such as cameras, binoculars, telescopes, and microscopes the reduction in reflections also improves the contrast of the image by elimination of stray light. This is especially important in planetary astronomy. In other applications, the primary benefit is the elimination of the reflection itself, such as a coating on eyeglass lenses that makes the eyes of the wearer more visible to others, or a coating to reduce the glint from a covert viewer's binoculars or telescopic sight.

In optics, a doublet is a type of lens made up of two simple lenses paired together. Such an arrangement allows more optical surfaces, thicknesses, and formulations, especially as the space between lenses may be considered an "element". With additional degrees of freedom, optical designers have more latitude to correct more optical aberrations more thoroughly.

A dielectric mirror, also known as a Bragg mirror, is a type of mirror composed of multiple thin layers of dielectric material, typically deposited on a substrate of glass or some other optical material. By careful choice of the type and thickness of the dielectric layers, one can design an optical coating with specified reflectivity at different wavelengths of light. Dielectric mirrors are also used to produce ultra-high reflectivity mirrors: values of 99.999% or better over a narrow range of wavelengths can be produced using special techniques. Alternatively, they can be made to reflect a broad spectrum of light, such as the entire visible range or the spectrum of the Ti-sapphire laser.

An optical fiber, or optical fibre, is a flexible glass or plastic fiber that can transmit light from one end to the other. Such fibers find wide usage in fiber-optic communications, where they permit transmission over longer distances and at higher bandwidths than electrical cables. Fibers are used instead of metal wires because signals travel along them with less loss and are immune to electromagnetic interference. Fibers are also used for illumination and imaging, and are often wrapped in bundles so they may be used to carry light into, or images out of confined spaces, as in the case of a fiberscope. Specially designed fibers are also used for a variety of other applications, such as fiber optic sensors and fiber lasers.

A refractometer is a laboratory or field device for the measurement of an index of refraction (refractometry). The index of refraction is calculated from the observed refraction angle using Snell's law. For mixtures, the index of refraction then allows the concentration to be determined using mixing rules such as the Gladstone–Dale relation and Lorentz–Lorenz equation.
Optical manufacturing and testing is the process of manufacturing and testing optical components. It spans a wide range of manufacturing procedures and optical test configurations.

Athermalization, in the field of optics, is the process of achieving optothermal stability in optomechanical systems. This is done by minimizing variations in optical performance over a range of temperatures.
The Christiansen effect is named after the Danish physicist Christian Christiansen and describes the reduced scattering of multi-phase microstructures at wavelengths where their refractive indices match.

Low-dispersion glass is a type of glass with reduced chromatic aberration, meaning the refractive index does not change as strongly with different wavelengths of light. In other words, the light passing through the glass has a smaller spread or dispersion between its constituent colors, resulting in a reduced "rainbow effect" at high-contrast edges. Wavelength dispersion in a certain material is characterized by its Abbe number; LD glass has a higher Abbe number than conventional types. Crown glass is an example of a relatively inexpensive low-dispersion glass.
Precision glass moulding is a replicative process that allows the production of high precision optical components from glass without grinding and polishing. The process is also known as ultra-precision glass pressing. It is used to manufacture precision glass lenses for consumer products such as digital cameras, and high-end products like medical systems. The main advantage over mechanical lens production is that complex lens geometries such as aspheres can be produced cost-efficiently.
Fiber-optic filter is an optical fiber instrument used for wavelength selection, which can select desired wavelengths to pass and reject the others. It is Widely used in DWDM systems dynamic wavelength selection, DWDM signal separation, optical performance monitoring, field tunable optical noise filtering and optical amplifier noise suppression, etc. Optical multiplexers (couplers) makes different wavelength coupling into an optical fiber and different wavelength carries different information. At the receiving end, if you want to separate desired wavelengths from optical fiber, it is necessary to use optical filter.

A lens antenna is a directional antenna that uses a shaped piece of microwave-transparent material to bend and focus microwaves by refraction, as an optical lens does for light. Typically it consists of a small feed antenna such as a patch antenna or horn antenna which radiates radio waves, with a piece of dielectric or composite material in front which functions as a converging lens to collimate the radio waves into a beam. Conversely, in a receiving antenna the lens focuses the incoming radio waves onto the feed antenna, which converts them to electric currents which are delivered to a radio receiver. They can also be fed by an array of feed antennas, called a focal plane array (FPA), to create more complicated radiation patterns.
Optical glass refers to a quality of glass suitable for the manufacture of optical systems such as optical lenses, prisms or mirrors. Unlike window glass or crystal, whose formula is adapted to the desired aesthetic effect, optical glass contains additives designed to modify certain optical or mechanical properties of the glass: refractive index, dispersion, transmittance, thermal expansion and other parameters. Lenses produced for optical applications use a wide variety of materials, from silica and conventional borosilicates to elements such as germanium and fluorite, some of which are essential for glass transparency in areas other than the visible spectrum.















