Glass batch calculation

Last updated April 04, 2019

Glass batch calculation or glass batching is used to determine the correct mix of raw materials (batch) for a glass melt.

Glass is a non-crystalline, amorphous solid that is often transparent and has widespread practical, technological, and decorative uses in, for example, window panes, tableware, and optoelectronics. The most familiar, and historically the oldest, types of manufactured glass are "silicate glasses" based on the chemical compound silica (silicon dioxide, or quartz), the primary constituent of sand. The term glass, in popular usage, is often used to refer only to this type of material, which is familiar from use as window glass and in glass bottles. Of the many silica-based glasses that exist, ordinary glazing and container glass is formed from a specific type called soda-lime glass, composed of approximately 75% silicon dioxide (SiO₂), sodium oxide (Na₂O) from sodium carbonate (Na₂CO₃), calcium oxide (CaO), also called lime, and several minor additives.

Principle

The raw materials mixture for glass melting is termed "batch". The batch must be measured properly to achieve a given, desired glass formulation. This batch calculation is based on the common linear regression equation:

In statistics, linear regression is a linear approach to modelling the relationship between a scalar response and one or more explanatory variables. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.

$N_{B}=(B^{T}\cdot B)^{-1}\cdot B^{T}\cdot N_{G}$

with N_B and N_G being the molarities 1-column matrices of the batch and glass components respectively, and B being the batching matrix.^[1]^[2]^[3] The symbol "^T" stands for the matrix transpose operation, "⁻¹" indicates matrix inversion, and the sign "·" means the scalar product. From the molarities matrices N, percentages by weight (wt%) can easily be derived using the appropriate molar masses.

Matrix (mathematics) Two-dimensional array of numbers with specific operations

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimensions of the matrix below are 2 × 3, because there are two rows and three columns:

In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal, that is it switches the row and column indices of the matrix by producing another matrix denoted as A^T. It is achieved by any one of the following equivalent actions:

In linear algebra, an n-by-n square matrix A is called invertible if there exists an n-by-n square matrix B such that

Example calculation

An example batch calculation may be demonstrated here. The desired glass composition in wt% is: 67 SiO₂, 12 Na₂O, 10 CaO, 5 Al₂O₃, 1 K₂O, 2 MgO, 3 B₂O₃, and as raw materials are used sand, trona, lime, albite, orthoclase, dolomite, and borax. The formulas and molar masses of the glass and batch components are listed in the following table:

Silicon dioxide, also known as silica, silicic acid or silicic acid anydride is an oxide of silicon with the chemical formula SiO₂, most commonly found in nature as quartz and in various living organisms. In many parts of the world, silica is the major constituent of sand. Silica is one of the most complex and most abundant families of materials, existing as a compound of several minerals and as synthetic product. Notable examples include fused quartz, fumed silica, silica gel, and aerogels. It is used in structural materials, microelectronics (as an electrical insulator), and as components in the food and pharmaceutical industries.

Sodium oxide is a chemical compound with the formula Na₂O. It is used in ceramics and glasses, though not in a raw form. It is the base anhydride of sodium hydroxide, so when water is added to sodium oxide NaOH is produced.

Calcium oxide (CaO), commonly known as quicklime or burnt lime, is a widely used chemical compound. It is a white, caustic, alkaline, crystalline solid at room temperature. The broadly used term lime connotes calcium-containing inorganic materials, in which carbonates, oxides and hydroxides of calcium, silicon, magnesium, aluminium, and iron predominate. By contrast, quicklime specifically applies to the single chemical compound calcium oxide. Calcium oxide that survives processing without reacting in building products such as cement is called free lime.

Formula of glass component	Desired concentration of glass component, wt%	Molar mass of glass component, g/mol	Batch component	Formula of batch component	Molar mass of batch component, g/mol
SiO₂	67	60.0843	Sand	SiO₂	60.0843
Na₂O	12	61.9789	Trona	Na₃H(CO₃)₂*2H₂O	226.0262
CaO	10	56.0774	Lime	CaCO₃	100.0872
Al₂O₃	5	101.9613	Albite	Na₂OAl₂O₃6SiO₂	524.4460
K₂O	1	94.1960	Orthoclase	K₂OAl₂O₃6SiO₂	556.6631
MgO	2	40.3044	Dolomite	MgCa(CO₃)₂	184.4014
B₂O₃	3	69.6202	Borax	Na₂B₄O₇*10H₂O	381.3721

The batching matrix B indicates the relation of the molarity in the batch (columns) and in the glass (rows). For example, the batch component SiO₂ adds 1 mol SiO₂ to the glass, therefore, the intersection of the first column and row shows "1". Trona adds 1.5 mol Na₂O to the glass; albite adds 6 mol SiO₂, 1 mol Na₂O, and 1 mol Al₂O₃, and so on. For the example given above, the complete batching matrix is listed below. The molarity matrix N_G of the glass is simply determined by dividing the desired wt% concentrations by the appropriate molar masses, e.g., for SiO₂ 67/60.0843 = 1.1151.

\mathbf {B} ={\begin{bmatrix}1&0&0&6&6&0&0\\0&1.5&0&1&0&0&1\\0&0&1&0&0&1&0\\0&0&0&1&1&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&2\end{bmatrix}}

\mathbf {N_{G}} ={\begin{bmatrix}1.1151\\0.1936\\0.1783\\0.0490\\0.0106\\0.0496\\0.0431\end{bmatrix}}

The resulting molarity matrix of the batch, N_B, is given here. After multiplication with the appropriate molar masses of the batch ingredients one obtains the batch mass fraction matrix M_B:

$\mathbf {N_{B}} ={\begin{bmatrix}0.82087\\0.08910\\0.12870\\0.03842\\0.01062\\0.04962\\0.02155\end{bmatrix}}$ $\mathbf {M_{B}} ={\begin{bmatrix}49.321\\20.138\\12.881\\20.150\\5.910\\9.150\\8.217\end{bmatrix}}$ or $\mathbf {M_{B}(100\%normalized)} ={\begin{bmatrix}39.216\\16.012\\10.242\\16.022\\4.699\\7.276\\6.533\end{bmatrix}}$

The matrix M_B, normalized to sum up to 100% as seen above, contains the final batch composition in wt%: 39.216 sand, 16.012 trona, 10.242 lime, 16.022 albite, 4.699 orthoclase, 7.276 dolomite, 6.533 borax. If this batch is melted to a glass, the desired composition given above is obtained.^[4] During glass melting, carbon dioxide (from trona, lime, dolomite) and water (from trona, borax) evaporate.

Carbon dioxide is a colorless gas with a density about 60% higher than that of dry air. Carbon dioxide consists of a carbon atom covalently double bonded to two oxygen atoms. It occurs naturally in Earth's atmosphere as a trace gas. The current concentration is about 0.04% (410 ppm) by volume, having risen from pre-industrial levels of 280 ppm. Natural sources include volcanoes, hot springs and geysers, and it is freed from carbonate rocks by dissolution in water and acids. Because carbon dioxide is soluble in water, it occurs naturally in groundwater, rivers and lakes, ice caps, glaciers and seawater. It is present in deposits of petroleum and natural gas. Carbon dioxide is odorless at normally encountered concentrations. However, at high concentrations, it has a sharp and acidic odor.

Water is a transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's streams, lakes, and oceans, and the fluids of most living organisms. It is vital for all known forms of life, even though it provides no calories or organic nutrients. Its chemical formula is H₂O, meaning that each of its molecules contains one oxygen and two hydrogen atoms, connected by covalent bonds. Water is the name of the liquid state of H₂O at standard ambient temperature and pressure. It forms precipitation in the form of rain and aerosols in the form of fog. Clouds are formed from suspended droplets of water and ice, its solid state. When finely divided, crystalline ice may precipitate in the form of snow. The gaseous state of water is steam or water vapor. Water moves continually through the water cycle of evaporation, transpiration (evapotranspiration), condensation, precipitation, and runoff, usually reaching the sea.

Simple glass batch calculation can be found at the website of the University of Washington.^[5]

Advanced batch calculation by optimization

If the number of glass and batch components is not equal, if it is impossible to exactly obtain the desired glass composition using the selected batch ingredients, or if the matrix equation is not soluble for other reasons (i.e., the rows/columns are linearly dependent), the batch composition must be determined by optimization techniques.

Related Research Articles

Stoichiometry is the calculation of reactants and products in chemical reactions.

In the theory of vector spaces, a set of vectors is said to be linearly dependent if at least one of the vectors in the set can be defined as a linear combination of the others; if no vector in the set can be written in this way, then the vectors are said to be linearly independent. These concepts are central to the definition of dimension.

An orthogonal matrix is a square matrix whose columns and rows are orthogonal unit vectors, i.e.

In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum.

In mathematics, matrix multiplication or matrix product is a binary operation that produces a matrix from two matrices with entries in a field, or, more generally, in a ring or even a semiring. The matrix product is designed for representing the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. In more detail, if $A$ is an $n \times m$ matrix and $B$ is an $m \times p$ matrix, their matrix product $AB$ is an $n \times p$ matrix, in which the $m$ entries across a row of $A$ are multiplied with the $m$ entries down a column of $B$ and summed to produce an entry of $AB$ . When two linear maps are represented by matrices, then the matrix product represents the composition of the two maps.

In linear algebra, the singular-value decomposition (SVD) is a factorization of a real or complex matrix. It is the generalization of the eigendecomposition of a positive semidefinite normal matrix to any $matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics.$

In chemistry, the molar massM is a physical property defined as the mass of a given substance divided by the amount of substance. The base SI unit for molar mass is kg/mol. However, for historical reasons, molar masses are almost always expressed in g/mol.

In mathematics, particularly in linear algebra, a skew-symmetricmatrix is a square matrix whose transpose equals its negative, that is, it satisfies the condition

In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. When the matrix is a square matrix, both the matrix and its determinant are referred to as the Jacobian in literature.

In the mathematical field of differential geometry, a metric tensor is a type of function which takes as input a pair of tangent vectors $v$ and $w$ at a point of a surface and produces a real number scalar $g (v, w)$ in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean space. In the same way as a dot product, metric tensors are used to define the length of and angle between tangent vectors. Through integration, the metric tensor allows one to define and compute the length of curves on the manifold.

Levinson recursion or Levinson–Durbin recursion is a procedure in linear algebra to recursively calculate the solution to an equation involving a Toeplitz matrix. The algorithm runs in Θ(n²) time, which is a strong improvement over Gauss–Jordan elimination, which runs in Θ(n³).

In linear algebra, a square matrix $is called diagonalizable or nondefective if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix such that is a diagonal matrix. If is a finite-dimensional vector space, then a linear map is called diagonalizable if there exists an ordered basis of with respect to which is represented by a diagonal matrix. Diagonalization is the process of finding a corresponding diagonal matrix for a diagonalizable matrix or linear map. A square matrix that is not diagonalizable is called defective.$

In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.

In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned.

In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables whose values evolve through time in a way that depends on the values they have at any given time and also depends on the externally imposed values of input variables. Output variables’ values depend on the values of the state variables.

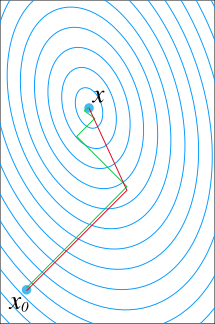
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.

In statistics, Bayesian multivariate linear regression is a Bayesian approach to multivariate linear regression, i.e. linear regression where the predicted outcome is a vector of correlated random variables rather than a single scalar random variable. A more general treatment of this approach can be found in the article MMSE estimator.

In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way.

References

↑ Y. B. Peng, Xingye Lei, D. E. Day: "A computer programme for optimising batch calculations"; Glass technology, vol. 32, 1991, no. 4, p 123–130.
↑ M. M. Khaimovich, K. Yu. Subbotin: "Automation of Batch Formula Calculation"; Glass and Ceramics, vol. 62, no 3-4, March 2005, p 109–112.
↑ A. I. Priven: "Calculating batch weights with a programmable microcalculator"; Glass and Ceramics, vol. 43, no 11, November 1986, p 488–491.
↑ See also: Free glass batch calculator
↑ "Glass Melting". Battelle PNNL MST Handbook. U.S. Department of Energy, Pacific Northwest Laboratory. Archived from the original on 2010-05-05. Retrieved 2008-01-26.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Y. B. Peng, Xingye Lei, D. E. Day: "A computer programme for optimising batch calculations"; Glass technology, vol. 32, 1991, no. 4, p 123–130.

[2] M. M. Khaimovich, K. Yu. Subbotin: "Automation of Batch Formula Calculation"; Glass and Ceramics, vol. 62, no 3-4, March 2005, p 109–112.

[3] A. I. Priven: "Calculating batch weights with a programmable microcalculator"; Glass and Ceramics, vol. 43, no 11, November 1986, p 488–491.

[4] See also: Free glass batch calculator

[5] "Glass Melting". Battelle PNNL MST Handbook. U.S. Department of Energy, Pacific Northwest Laboratory. Archived from the original on 2010-05-05. Retrieved 2008-01-26.

v t e Glass science topics
Basics	Glass Glass transition Supercooling
Formulation	AgInSbTe Bioglass Borophosphosilicate glass Borosilicate glass Ceramic glaze Chalcogenide glass Cobalt glass Cranberry glass Crown glass Flint glass Fluorosilicate glass Fused quartz GeSbTe Gold ruby glass Lead glass Milk glass Phosphosilicate glass Photochromic lens glass Silicate glass Soda–lime glass Sodium hexametaphosphate Soluble glass Tellurite glass Thoriated glass Ultra low expansion glass Uranium glass Vitreous enamel Wood's glass ZBLAN
Glass-ceramics	Bioactive glass CorningWare Glass-ceramic-to-metal seals Macor Zerodur
Preparation	Annealing Chemical vapor deposition Glass batch calculation Glass forming Glass melting Glass modeling Ion implantation Liquidus temperature Sol-gel technique Viscosity Vitrification
Optics	Achromat Dispersion Gradient-index optics Hydrogen darkening Optical amplifier Optical fiber Optical lens design Photochromic lens Photosensitive glass Refraction Transparent materials
Surface modification	Anti-reflective coating Chemically strengthened glass Corrosion Dealkalization DNA microarray Hydrogen darkening Insulated glazing Porous glass Self-cleaning glass Sol-gel technique Tempered glass
Diverse topics	Glass-coated wire Safety glass Glass databases Glass electrode Glass fiber reinforced concrete Glass ionomer cement Glass microspheres Glass-reinforced plastic Glass-to-metal seal Porous glass Prince Rupert's drops Radioactive waste vitrification Windshield Glass fiber