In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering, mostly as a tool for solving linear differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions f, the Laplace transform is defined by the integral

Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

A random variable is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' can be misleading as its mathematical definition is not actually random nor a variable, but rather it is a function from possible outcomes in a sample space to a measurable space, often to the real numbers.

In probability theory, a probability space or a probability triple is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die.
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behavior can be characterized: two readily understood behaviors are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.

In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.
In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, S. Watanabe, I. Shigekawa, and so on finally completed the foundations.
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices, random growth models or physical systems that are subjected to thermal fluctuations.
In mathematics, probabilistic metric spaces are a generalization of metric spaces where the distance no longer takes values in the non-negative real numbers R ≥ 0, but in distribution functions.
In mathematics, a π-system on a set is a collection of certain subsets of such that
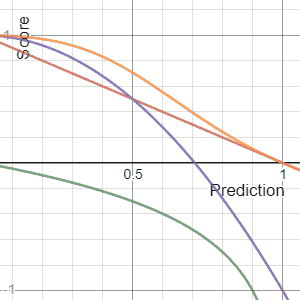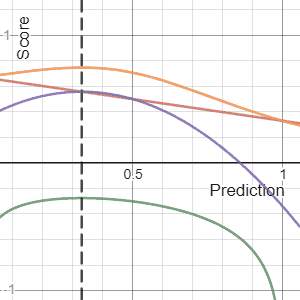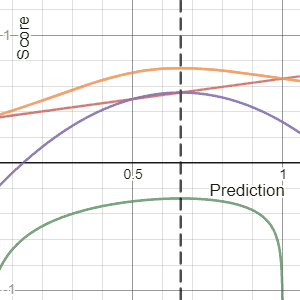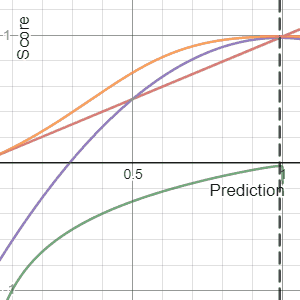
In decision theory, a scoring rule provides a summary measure for the evaluation of probabilistic predictions or forecasts. It is applicable to tasks in which predictions assign probabilities to events, i.e. one issues a probability distribution as prediction. This includes probabilistic classification of a set of mutually exclusive outcomes or classes.
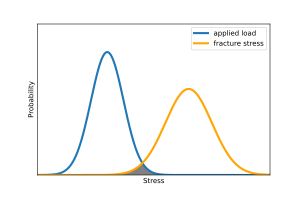
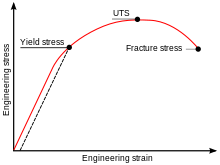
Uncertainty quantification (UQ) is the science of quantitative characterization and estimation of uncertainties in both computational and real world applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known. An example would be to predict the acceleration of a human body in a head-on crash with another car: even if the speed was exactly known, small differences in the manufacturing of individual cars, how tightly every bolt has been tightened, etc., will lead to different results that can only be predicted in a statistical sense.
In probability theory, a standard probability space, also called Lebesgue–Rokhlin probability space or just Lebesgue space is a probability space satisfying certain assumptions introduced by Vladimir Rokhlin in 1940. Informally, it is a probability space consisting of an interval and/or a finite or countable number of atoms.
In mathematics – specifically, in the theory of stochastic processes – Doob's martingale convergence theorems are a collection of results on the limits of supermartingales, named after the American mathematician Joseph L. Doob. Informally, the martingale convergence theorem typically refers to the result that any supermartingale satisfying a certain boundedness condition must converge. One may think of supermartingales as the random variable analogues of non-increasing sequences; from this perspective, the martingale convergence theorem is a random variable analogue of the monotone convergence theorem, which states that any bounded monotone sequence converges. There are symmetric results for submartingales, which are analogous to non-decreasing sequences.

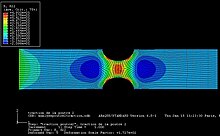
In numerical analysis, the interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics, composite structures, biomechanics and in many other areas. The goal of the Interval Finite Element is to find upper and lower bounds of different characteristics of the model and use these results in the design process. This is so called worst case design, which is closely related to the limit state design.
In probability theory, the Doob–Dynkin lemma, named after Joseph L. Doob and Eugene Dynkin, characterizes the situation when one random variable is a function of another by the inclusion of the -algebras generated by the random variables. The usual statement of the lemma is formulated in terms of one random variable being measurable with respect to the -algebra generated by the other.

A probability box is a characterization of uncertain numbers consisting of both aleatoric and epistemic uncertainties that is often used in risk analysis or quantitative uncertainty modeling where numerical calculations must be performed. Probability bounds analysis is used to make arithmetic and logical calculations with p-boxes.
Probability bounds analysis (PBA) is a collection of methods of uncertainty propagation for making qualitative and quantitative calculations in the face of uncertainties of various kinds. It is used to project partial information about random variables and other quantities through mathematical expressions. For instance, it computes sure bounds on the distribution of a sum, product, or more complex function, given only sure bounds on the distributions of the inputs. Such bounds are called probability boxes, and constrain cumulative probability distributions.
Line sampling is a method used in reliability engineering to compute small failure probabilities encountered in engineering systems. The method is particularly suitable for high-dimensional reliability problems, in which the performance function exhibits moderate non-linearity with respect to the uncertain parameters The method is suitable for analyzing black box systems, and unlike the importance sampling method of variance reduction, does not require detailed knowledge of the system.