Examples
Bernoulli model
The Bernoulli model admits a complete statistic. [1] Let X be a random sample of size n such that each Xi has the same Bernoulli distribution with parameter p. Let T be the number of 1s observed in the sample, i.e.  . T is a statistic of X which has a binomial distribution with parameters (n,p). If the parameter space for p is (0,1), then T is a complete statistic. To see this, note that
. T is a statistic of X which has a binomial distribution with parameters (n,p). If the parameter space for p is (0,1), then T is a complete statistic. To see this, note that

Observe also that neither p nor 1 − p can be 0. Hence  if and only if:
if and only if:

On denoting p/(1 − p) by r, one gets:

First, observe that the range of r is the positive reals. Also, E(g(T)) is a polynomial in r and, therefore, can only be identical to 0 if all coefficients are 0, that is, g(t) = 0 for all t.
It is important to notice that the result that all coefficients must be 0 was obtained because of the range of r. Had the parameter space been finite and with a number of elements less than or equal to n, it might be possible to solve the linear equations in g(t) obtained by substituting the values of r and get solutions different from 0. For example, if n = 1 and the parameter space is {0.5}, a single observation and a single parameter value, T is not complete. Observe that, with the definition:

then, E(g(T)) = 0 although g(t) is not 0 for t = 0 nor for t = 1.
Gaussian model with fixed variance
This example will show that, in a sample X1, X2 of size 2 from a normal distribution with known variance, the statistic X1 + X2 is complete and sufficient. Suppose X1, X2 are independent, identically distributed random variables, normally distributed with expectation θ and variance 1. The sum

is a complete statistic for θ.
To show this, it is sufficient to demonstrate that there is no non-zero function  such that the expectation of
such that the expectation of

remains zero regardless of the value of θ.
That fact may be seen as follows. The probability distribution of X1 + X2 is normal with expectation 2θ and variance 2. Its probability density function in  is therefore proportional to
is therefore proportional to

The expectation of g above would therefore be a constant times

A bit of algebra reduces this to

where k(θ) is nowhere zero and

As a function of θ this is a two-sided Laplace transform of h, and cannot be identically zero unless h is zero almost everywhere. [2] The exponential is not zero, so this can only happen if g is zero almost everywhere.
By contrast, the statistic  is sufficient but not complete. It admits a non-zero unbiased estimator of zero, namely
is sufficient but not complete. It admits a non-zero unbiased estimator of zero, namely  .
.
Sufficiency does not imply completeness
Most parametric models have a sufficient statistic which is not complete. This is important because the Lehmann–Scheffé theorem cannot be applied to such models. Galili and Meilijson 2016 [3] propose the following didactic example.
Consider  independent samples from the uniform distribution:
independent samples from the uniform distribution:

 is a known design parameter. This model is a scale family (a specific case of a location-scale family) model: scaling the samples by a multiplier
is a known design parameter. This model is a scale family (a specific case of a location-scale family) model: scaling the samples by a multiplier  multiplies the parameter
multiplies the parameter  .
.
Galili and Meilijson show that the minimum and maximum of the samples are together a sufficient statistic:  (using the usual notation for order statistics). Indeed, conditional on these two values, the distribution of the rest of the sample is simply uniform on the range they define:
(using the usual notation for order statistics). Indeed, conditional on these two values, the distribution of the rest of the sample is simply uniform on the range they define:  .
.
However, their ratio has a distribution which does not depend on  . This follows from the fact that this is a scale family: any change of scale impacts both variables identically. Subtracting the mean
. This follows from the fact that this is a scale family: any change of scale impacts both variables identically. Subtracting the mean  from that distribution, we obtain:
from that distribution, we obtain:

We have thus shown that there exists a function  which is not
which is not  everywhere but which has expectation
everywhere but which has expectation  . The pair is thus not complete.
. The pair is thus not complete.
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule, the quantity of interest and its result are distinguished. For example, the sample mean is a commonly used estimator of the population mean.
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.
In statistics, sufficiency is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. A sufficient statistic contains all of the information that the dataset provides about the model parameters. It is closely related to the concepts of an ancillary statistic which contains no information about the model parameters, and of a complete statistic which only contains information about the parameters and no ancillary information.
In statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter. More formally, it is the application of a point estimator to the data to obtain a point estimate.
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the true value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk, as an estimate of the true MSE.
In statistics, the Lehmann–Scheffé theorem is a prominent statement, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation. The theorem states that any estimator that is unbiased for a given unknown quantity and that depends on the data only through a complete, sufficient statistic is the unique best unbiased estimator of that quantity. The Lehmann–Scheffé theorem is named after Erich Leo Lehmann and Henry Scheffé, given their two early papers.
In statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result that characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar criteria.
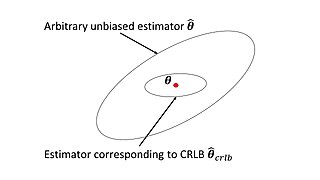
In estimation theory and statistics, the Cramér–Rao bound (CRB) relates to estimation of a deterministic parameter. The result is named in honor of Harald Cramér and Calyampudi Radhakrishna Rao, but has also been derived independently by Maurice Fréchet, Georges Darmois, and by Alexander Aitken and Harold Silverstone. It is also known as Fréchet-Cramér–Rao or Fréchet-Darmois-Cramér-Rao lower bound. It states that the precision of any unbiased estimator is at most the Fisher information; or (equivalently) the reciprocal of the Fisher information is a lower bound on its variance.
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.

In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter θ0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to θ0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to θ0 converges to one.
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An estimator attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered:
In statistics a minimum-variance unbiased estimator (MVUE) or uniformly minimum-variance unbiased estimator (UMVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.
In econometrics and statistics, the generalized method of moments (GMM) is a generic method for estimating parameters in statistical models. Usually it is applied in the context of semiparametric models, where the parameter of interest is finite-dimensional, whereas the full shape of the data's distribution function may not be known, and therefore maximum likelihood estimation is not applicable.
Bootstrapping is a procedure for estimating the distribution of an estimator by resampling one's data or a model estimated from the data. Bootstrapping assigns measures of accuracy to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods.
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function. Equivalently, it maximizes the posterior expectation of a utility function. An alternative way of formulating an estimator within Bayesian statistics is maximum a posteriori estimation.
In statistics, Basu's theorem states that any boundedly complete minimal sufficient statistic is independent of any ancillary statistic. This is a 1955 result of Debabrata Basu.
In statistics, the bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. In statistics, "bias" is an objective property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased.
In statistics and in particular statistical theory, unbiased estimation of a standard deviation is the calculation from a statistical sample of an estimated value of the standard deviation of a population of values, in such a way that the expected value of the calculation equals the true value. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the use of significance tests and confidence intervals, or by using Bayesian analysis.
In statistics, Fisher consistency, named after Ronald Fisher, is a desirable property of an estimator asserting that if the estimator were calculated using the entire population rather than a sample, the true value of the estimated parameter would be obtained.
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An efficient estimator is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense.





























