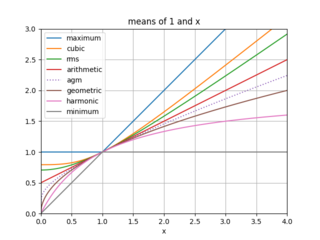
In mathematics, the Heinz mean (named after E. Heinz [1] ) of two non-negative real numbers A and B, was defined by Bhatia [2] as:
with 0 ≤ x ≤ 1/2.
For different values of x, this Heinz mean interpolates between the arithmetic (x = 0) and geometric (x = 1/2) means such that for 0 < x < 1/2:
The Heinz means appear naturally when symmetrizing -divergences. [3]
It may also be defined in the same way for positive semidefinite matrices, and satisfies a similar interpolation formula. [4] [5]
In mathematics, the arithmetic–geometric mean of two positive real numbers x and y is the mutual limit of a sequence of arithmetic means and a sequence of geometric means. The arithmetic–geometric mean is used in fast algorithms for exponential, trigonometric functions, and other special functions, as well as some mathematical constants, in particular, computing π.
In mathematics, the determinant is a scalar-valued function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the linear map represented, on a given basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map is an isomorphism.
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of positive real numbers by using the product of their values. The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, ..., an, the geometric mean is defined as
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.
The median of a set of numbers is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as the “middle" value. The basic feature of the median in describing data compared to the mean is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of the center. Median income, for example, may be a better way to describe the center of the income distribution because increases in the largest incomes alone have no effect on the median. For this reason, the median is of central importance in robust statistics.
The Cauchy–Schwarz inequality is an upper bound on the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics.
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or in terms of two positive parameters, denoted by alpha (α) and beta (β), that appear as exponents of the variable and its complement to 1, respectively, and control the shape of the distribution.
In the mathematical discipline of linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices. There are many different matrix decompositions; each finds use among a particular class of problems.
In linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. The Householder transformation was used in a 1958 paper by Alston Scott Householder.
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements only on the main diagonal, the subdiagonal/lower diagonal, and the supradiagonal/upper diagonal. For example, the following matrix is tridiagonal:
In mathematics and statistics, the quasi-arithmetic mean or generalised f-mean or Kolmogorov-Nagumo-de Finetti mean is one generalisation of the more familiar means such as the arithmetic mean and the geometric mean, using a function . It is also called Kolmogorov mean after Soviet mathematician Andrey Kolmogorov. It is a broader generalization than the regular generalized mean.
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same.
In mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.
In mathematics, the three classical Pythagorean means are the arithmetic mean (AM), the geometric mean (GM), and the harmonic mean (HM). These means were studied with proportions by Pythagoreans and later generations of Greek mathematicians because of their importance in geometry and music.
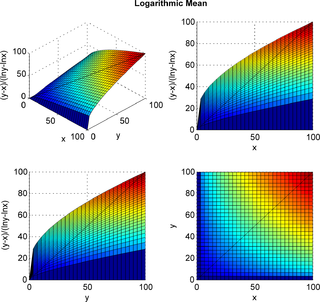
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer.
Simple rational approximation (SRA) is a subset of interpolating methods using rational functions. Especially, SRA interpolates a given function with a specific rational function whose poles and zeros are simple, which means that there is no multiplicity in poles and zeros. Sometimes, it only implies simple poles.
In mathematics, a contraharmonic mean is a function complementary to the harmonic mean. The contraharmonic mean is a special case of the Lehmer mean, , where p = 2.
In mathematics and statistics, the Fréchet mean is a generalization of centroids to metric spaces, giving a single representative point or central tendency for a cluster of points. It is named after Maurice Fréchet. Karcher mean is the renaming of the Riemannian Center of Mass construction developed by Karsten Grove and Hermann Karcher. On the real numbers, the arithmetic mean, median, geometric mean, and harmonic mean can all be interpreted as Fréchet means for different distance functions.
In mathematics, there are many kinds of inequalities involving matrices and linear operators on Hilbert spaces. This article covers some important operator inequalities connected with traces of matrices.
In mathematics of special functions, the Neuman–Sándor meanM, of two positive and unequal numbers a and b, is defined as:
 | This applied mathematics-related article is a stub. You can help Wikipedia by expanding it. |
