
In welfare economics, a Pareto improvement formalizes the idea of an outcome being "better in every possible way". A change is called a Pareto improvement if it leaves everyone in a society better-off. A situation is called Pareto efficient or Pareto optimal if all possible Pareto improvements have already been made; in other words, there are no longer any ways left to make one person better-off, without making some other person worse-off.
In economics, utility is a measure of the satisfaction that a certain person has from a certain state of the world. Over time, the term has been used in at least two different meanings.
Satisficing is a decision-making strategy or cognitive heuristic that entails searching through the available alternatives until an acceptability threshold is met. The term satisficing, a portmanteau of satisfy and suffice, was introduced by Herbert A. Simon in 1956, although the concept was first posited in his 1947 book Administrative Behavior. Simon used satisficing to explain the behavior of decision makers under circumstances in which an optimal solution cannot be determined. He maintained that many natural problems are characterized by computational intractability or a lack of information, both of which preclude the use of mathematical optimization procedures. He observed in his Nobel Prize in Economics speech that "decision makers can satisfice either by finding optimum solutions for a simplified world, or by finding satisfactory solutions for a more realistic world. Neither approach, in general, dominates the other, and both have continued to co-exist in the world of management science".

In mathematical optimization and decision theory, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite, in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy.
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour.
In signal processing, the output of the matched filter is given by correlating a known delayed signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template. The matched filter is the optimal linear filter for maximizing the signal-to-noise ratio (SNR) in the presence of additive stochastic noise.
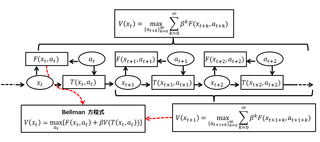
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior distribution over the quantity one wants to estimate. MAP estimation can therefore be seen as a regularization of maximum likelihood estimation.

In probability theory, the Kelly criterion is a formula for sizing a sequence of bets by maximizing the long-term expected value of the logarithm of wealth, which is equivalent to maximizing the long-term expected geometric growth rate. John Larry Kelly Jr., a researcher at Bell Labs, described the criterion in 1956.
In statistics, M-estimators are a broad class of extremum estimators for which the objective function is a sample average. Both non-linear least squares and maximum likelihood estimation are special cases of M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new types of M-estimators. However, M-estimators are not inherently robust, as is clear from the fact that they include maximum likelihood estimators, which are in general not robust. The statistical procedure of evaluating an M-estimator on a data set is called M-estimation.
In decision theory, the expected value of sample information (EVSI) is the expected increase in utility that a decision-maker could obtain from gaining access to a sample of additional observations before making a decision. The additional information obtained from the sample may allow them to make a more informed, and thus better, decision, thus resulting in an increase in expected utility. EVSI attempts to estimate what this improvement would be before seeing actual sample data; hence, EVSI is a form of what is known as preposterior analysis. The use of EVSI in decision theory was popularized by Robert Schlaifer and Howard Raiffa in the 1960s.

Revenue equivalence is a concept in auction theory that states that given certain conditions, any mechanism that results in the same outcomes also has the same expected revenue.
Causal decision theory (CDT) is a school of thought within decision theory which states that, when a rational agent is confronted with a set of possible actions, one should select the action which causes the best outcome in expectation. CDT contrasts with evidential decision theory (EDT), which recommends the action which would be indicative of the best outcome if one received the "news" that it had been taken. In other words, EDT recommends to "do what you most want to learn that you will do."

In decision theory, the von Neumann–Morgenstern (VNM) utility theorem demonstrates that rational choice under uncertainty involves making decisions that take the form of maximizing the expected value of some cardinal utility function. This function is known as the von Neumann–Morgenstern utility function. The theorem forms the foundation of expected utility theory.
In decision theory and quantitative policy analysis, the expected value of including uncertainty (EVIU) is the expected difference in the value of a decision based on a probabilistic analysis versus a decision based on an analysis that ignores uncertainty.
In mechanism design, a Vickrey–Clarke–Groves (VCG) mechanism is a generic truthful mechanism for achieving a socially optimal solution. It is a generalization of a Vickrey–Clarke–Groves auction. A VCG auction performs a specific task: dividing items among people. A VCG mechanism is more general: it can be used to select any outcome out of a set of possible outcomes.
A random-sampling mechanism (RSM) is a truthful mechanism that uses sampling in order to achieve approximately-optimal gain in prior-free mechanisms and prior-independent mechanisms.
A Bayesian-optimal mechanism (BOM) is a mechanism in which the designer does not know the valuations of the agents for whom the mechanism is designed, but the designer knows that they are random variables and knows the probability distribution of these variables.
Dynamic discrete choice (DDC) models, also known as discrete choice models of dynamic programming, model an agent's choices over discrete options that have future implications. Rather than assuming observed choices are the result of static utility maximization, observed choices in DDC models are assumed to result from an agent's maximization of the present value of utility, generalizing the utility theory upon which discrete choice models are based.
In the mathematical subjects of information theory and decision theory, Blackwell's informativeness theorem is an important result related to the ranking of information structures, or experiments. It states that there is an equivalence between three possible rankings of information structures: one based in expected utility, one based in informativeness, and one based in feasibility. This ranking defines a partial order over information structures known as the Blackwell order, or Blackwell's criterion.





















