
Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".

Computer-aided design (CAD) is the use of computers to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve communications through documentation, and to create a database for manufacturing. Designs made through CAD software help protect products and inventions when used in patent applications. CAD output is often in the form of electronic files for print, machining, or other manufacturing operations. The terms computer-aided drafting (CAD) and computer-aided design and drafting (CADD) are also used.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

In vector computer graphics, CAD systems, and geographic information systems, geometric primitive is the simplest geometric shape that the system can handle. Sometimes the subroutines that draw the corresponding objects are called "geometric primitives" as well. The most "primitive" primitives are point and straight line segment, which were all that early vector graphics systems had.

Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in computer graphics for representing curves and surfaces. It offers great flexibility and precision for handling both analytic and modeled shapes. It is a type of curve modeling, as opposed to polygonal modeling or digital sculpting. NURBS curves are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE). They are part of numerous industry-wide standards, such as IGES, STEP, ACIS, and PHIGS. Tools for creating and editing NURBS surfaces are found in various 3D graphics, rendering, and animation software packages.

Digital geometry deals with discrete sets considered to be digitized models or images of objects of the 2D or 3D Euclidean space. Simply put, digitizing is replacing an object by a discrete set of its points. The images we see on the TV screen, the raster display of a computer, or in newspapers are in fact digital images.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

Constructive solid geometry is a technique used in solid modeling. Constructive solid geometry allows a modeler to create a complex surface or object by using Boolean operators to combine simpler objects, potentially generating visually complex objects by combining a few primitive ones.

Solid modeling is a consistent set of principles for mathematical and computer modeling of three-dimensional shapes (solids). Solid modeling is distinguished within the broader related areas of geometric modeling and computer graphics, such as 3D modeling, by its emphasis on physical fidelity. Together, the principles of geometric and solid modeling form the foundation of 3D-computer-aided design, and in general, support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.
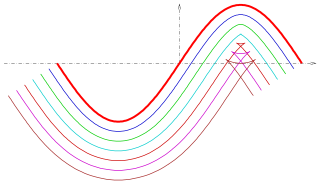
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of parallel (straight) lines. It can also be defined as a curve whose points are at a constant normal distance from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not.

In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice for real-time computer graphics. Alternate methods of representing 3D objects include NURBS surfaces, subdivision surfaces, and equation-based representations used in ray tracers.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.
Geometric modeling is a branch of applied mathematics and computational geometry that studies methods and algorithms for the mathematical description of shapes. The shapes studied in geometric modeling are mostly two- or three-dimensional, although many of its tools and principles can be applied to sets of any finite dimension. Today most geometric modeling is done with computers and for computer-based applications. Two-dimensional models are important in computer typography and technical drawing. Three-dimensional models are central to computer-aided design and manufacturing (CAD/CAM), and widely used in many applied technical fields such as civil and mechanical engineering, architecture, geology and medical image processing.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.
Function Representation is used in solid modeling, volume modeling and computer graphics. FRep was introduced in "Function representation in geometric modeling: concepts, implementation and applications" as a uniform representation of multidimensional geometric objects (shapes). An object as a point set in multidimensional space is defined by a single continuous real-valued function of point coordinates which is evaluated at the given point by a procedure traversing a tree structure with primitives in the leaves and operations in the nodes of the tree. The points with belong to the object, and the points with are outside of the object. The point set with is called an isosurface.

Computer graphics is a sub-field of computer science which studies methods for digitally synthesizing and manipulating visual content. Although the term often refers to the study of three-dimensional computer graphics, it also encompasses two-dimensional graphics and image processing.

Cobalt is a parametric-based computer-aided design (CAD) and 3D modeling program that runs on both Macintosh and Microsoft Windows operating systems. The program combines the direct-modeling way to create and edit objects and the highly structured, history-driven parametric way exemplified by programs like Pro/ENGINEER. A product of Ashlar-Vellum, Cobalt is Wireframe-based and history-driven with associativity and 2D equation-driven parametrics and constraints. It offers surfacing tools, mold design tools, detailing, and engineering features. Cobalt includes a library of 149,000 mechanical parts.

In 3D computer graphics, 3D modeling is the process of developing a mathematical coordinate-based representation of a surface of an object in three dimensions via specialized software by manipulating edges, vertices, and polygons in a simulated 3D space.

















