
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
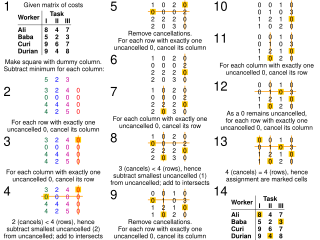
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows:

The Bellman–Ford algorithm is an algorithm that computes shortest paths from a single source vertex to all of the other vertices in a weighted digraph. It is slower than Dijkstra's algorithm for the same problem, but more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers. The algorithm was first proposed by Alfonso Shimbel, but is instead named after Richard Bellman and Lester Ford Jr., who published it in 1958 and 1956, respectively. Edward F. Moore also published a variation of the algorithm in 1959, and for this reason it is also sometimes called the Bellman–Ford–Moore algorithm.

In optimization theory, maximum flow problems involve finding a feasible flow through a flow network that obtains the maximum possible flow rate.

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. In other words, a subset of the edges is a matching if each vertex appears in at most one edge of that matching. Finding a matching in a bipartite graph can be treated as a network flow problem.
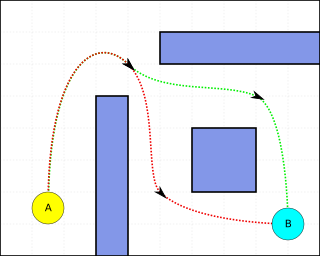
Pathfinding or pathing is the search, by a computer application, for the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
In computer science, the Hopcroft–Karp algorithm is an algorithm that takes a bipartite graph as input and produces a maximum-cardinality matching as output — a set of as many edges as possible with the property that no two edges share an endpoint. It runs in time in the worst case, where is set of edges in the graph, is set of vertices of the graph, and it is assumed that . In the case of dense graphs the time bound becomes , and for sparse random graphs it runs in time with high probability.
Maximum cardinality matching is a fundamental problem in graph theory. We are given a graph G, and the goal is to find a matching containing as many edges as possible; that is, a maximum cardinality subset of the edges such that each vertex is adjacent to at most one edge of the subset. As each edge will cover exactly two vertices, this problem is equivalent to the task of finding a matching that covers as many vertices as possible.
The minimum-cost flow problem (MCFP) is an optimization and decision problem to find the cheapest possible way of sending a certain amount of flow through a flow network. A typical application of this problem involves finding the best delivery route from a factory to a warehouse where the road network has some capacity and cost associated. The minimum cost flow problem is one of the most fundamental among all flow and circulation problems because most other such problems can be cast as a minimum cost flow problem and also that it can be solved efficiently using the network simplex algorithm.

Dimitri Panteli Bertsekas is an applied mathematician, electrical engineer, and computer scientist, a McAfee Professor at the Department of Electrical Engineering and Computer Science in School of Engineering at the Massachusetts Institute of Technology (MIT), Cambridge, Massachusetts, and also a Fulton Professor of Computational Decision Making at Arizona State University, Tempe.
In graph theory, the blossom algorithm is an algorithm for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph G = (V, E), the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph.

Paul Tseng was a Chinese-American and Canadian applied mathematician and a professor at the Department of Mathematics at the University of Washington, in Seattle, Washington. Tseng was recognized by his peers to be one of the leading optimization researchers of his generation. On August 13, 2009, Paul Tseng went missing while kayaking in the Jinsha River in the Yunnan province of China and is presumed dead.

In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
In mathematical optimization, the network simplex algorithm is a graph theoretic specialization of the simplex algorithm. The algorithm is usually formulated in terms of a minimum-cost flow problem. The network simplex method works very well in practice, typically 200 to 300 times faster than the simplex method applied to general linear program of same dimensions.











