
A steam turbine or steam turbine engine is a machine or heat engine that extracts thermal energy from pressurized steam and uses it to do mechanical work on a rotating output shaft. Its modern manifestation was invented by Charles Parsons in 1884. Fabrication of a modern steam turbine involves advanced metalwork to form high-grade steel alloys into precision parts using technologies that first became available in the 20th century; continued advances in durability and efficiency of steam turbines remains central to the energy economics of the 21st century.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as or where is the Laplace operator, is the divergence operator, is the gradient operator, and is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
Blade element theory (BET) is a mathematical process originally designed by William Froude (1878), David W. Taylor (1893) and Stefan Drzewiecki (1885) to determine the behavior of propellers. It involves breaking a blade down into several small parts then determining the forces on each of these small blade elements. These forces are then integrated along the entire blade and over one rotor revolution in order to obtain the forces and moments produced by the entire propeller or rotor. One of the key difficulties lies in modelling the induced velocity on the rotor disk. Because of this the blade element theory is often combined with momentum theory to provide additional relationships necessary to describe the induced velocity on the rotor disk, producing blade element momentum theory. At the most basic level of approximation a uniform induced velocity on the disk is assumed:
Particle velocity is the velocity of a particle in a medium as it transmits a wave. The SI unit of particle velocity is the metre per second (m/s). In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string.

An axial compressor is a gas compressor that can continuously pressurize gases. It is a rotating, airfoil-based compressor in which the gas or working fluid principally flows parallel to the axis of rotation, or axially. This differs from other rotating compressors such as centrifugal compressor, axi-centrifugal compressors and mixed-flow compressors where the fluid flow will include a "radial component" through the compressor.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z).
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.
In non ideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.
In turbomachinery, degree of reaction or reaction ratio is defined as the ratio of the change in static pressure in the rotating blades of a compressor or turbine, to the static pressure change in the compressor or turbine stage. Alternatively it is the ratio of static enthalpy change in the rotor to the static enthalpy change in the stage.
Compressor characteristic is a mathematical curve that shows the behaviour of a fluid going through a dynamic compressor. It shows changes in fluid pressure, temperature, entropy, flow rate etc.) with the compressor operating at different speeds.
Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.
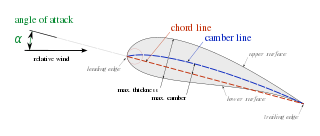
Blade solidity is an important design parameter for the axial flow impeller and is defined as the ratio of blade chord length to spacing.
Flotation of flexible objects is a phenomenon in which the bending of a flexible material allows an object to displace a greater amount of fluid than if it were completely rigid. This ability to displace more fluid translates directly into an ability to support greater loads, giving the flexible structure an advantage over a similarly rigid one. Inspiration to study the effects of elasticity are taken from nature, where plants, such as black pepper, and animals living at the water surface have evolved to take advantage of the load-bearing benefits elasticity imparts.
Propeller theory is the science governing the design of efficient propellers. A propeller is the most common propulsor on ships, and on small aircraft.
The Izbash formula is a mathematical expression used to calculate the stability of armourstone in flowing water environments.









































