In combinatorial mathematics, a de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring (i.e., as a contiguous subsequence). Such a sequence is denoted by B(k, n) and has length kn, which is also the number of distinct strings of length n on A. Each of these distinct strings, when taken as a substring of B(k, n), must start at a different position, because substrings starting at the same position are not distinct. Therefore, B(k, n) must have at leastkn symbols. And since B(k, n) has exactlykn symbols, de Bruijn sequences are optimally short with respect to the property of containing every string of length n at least once.
Contents
- History
- Examples
- Construction
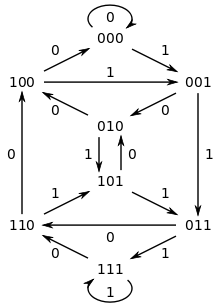
- Example using de Bruijn graph
- Example using inverse Burrows—Wheeler transform
- Algorithm
- Uses
- Angle detection
- Finding least- or most-significant set bit in a word
- Brute-force attacks on locks
- f-fold de Bruijn sequences
- de Bruijn torus
- de Bruijn decoding
- See also
- Notes
- References
- External links
The number of distinct de Bruijn sequences B(k, n) is
For a binary alphabet this is , leading to the following sequence for positive : 1, 1, 2, 16, 2048, 67108864... ( OEIS: A016031 )
The sequences are named after the Dutch mathematician Nicolaas Govert de Bruijn, who wrote about them in 1946. [1] As he later wrote, [2] the existence of de Bruijn sequences for each order together with the above properties were first proved, for the case of alphabets with two elements, by CamilleFlye Sainte-Marie ( 1894 ). The generalization to larger alphabets is due to Tatyanavan Aardenne-Ehrenfest andde Bruijn ( 1951 ). Automata for recognizing these sequences are denoted as de Bruijn automata.
In many applications, A = {0,1}.