 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these messages)
|
The Hagen number (Hg) is a dimensionless number used in forced flow calculations. It is the forced flow equivalent of the Grashof number and was named after the German hydraulic engineer G. H. L. Hagen.
It is defined as:
where:
For natural convection
and so the Hagen number then coincides with the Grashof number.
Awad: [1] presented Hagen number vs. Bejan number. Although their physical meaning is not the same because the former represents the dimensionless pressure gradient while the latter represents the dimensionless pressure drop, it will be shown that Hagen number coincides with Bejan number in cases where the characteristic length (l) is equal to the flow length (L). Also, a new expression of Bejan number in the Hagen-Poiseuille flow will be introduced. In addition, extending the Hagen number to a general form will be presented. For the case of Reynolds analogy (Pr = Sc = 1), all these three definitions of Hagen number will be the same. The general form of the Hagen number is
where
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:
In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.
In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.
In viscous fluid dynamics, the Archimedes number (Ar), is a dimensionless number used to determine the motion of fluids due to density differences, named after the ancient Greek scientist and mathematician Archimedes.
The Richardson number (Ri) is named after Lewis Fry Richardson (1881–1953). It is the dimensionless number that expresses the ratio of the buoyancy term to the flow shear term:
Darcy's law is an equation that describes the flow of a fluid through a porous medium and through a Hele-Shaw cell. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference via the hydraulic conductivity. In fact, the Darcy's law is a special case of the Stokes equation for the momentum flux, in turn deriving from the momentum Navier-Stokes equation.
The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the (− + + +) metric signature, the gravitational part of the action is given as
There are two different Bejan numbers (Be) used in the scientific domains of thermodynamics and fluid mechanics. Bejan numbers are named after Adrian Bejan.
Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.
The Stanton number, St, is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid. The Stanton number is named after Thomas Stanton (engineer) (1865–1931). It is used to characterize heat transfer in forced convection flows.
The Euler number (Eu) is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop caused by a restriction and the kinetic energy per volume of the flow, and is used to characterize energy losses in the flow, where a perfect frictionless flow corresponds to an Euler number of 0. The inverse of the Euler number is referred to as the Ruark Number with the symbol Ru.
The Womersley number is a dimensionless number in biofluid mechanics and biofluid dynamics. It is a dimensionless expression of the pulsatile flow frequency in relation to viscous effects. It is named after John R. Womersley (1907–1958) for his work with blood flow in arteries. The Womersley number is important in keeping dynamic similarity when scaling an experiment. An example of this is scaling up the vascular system for experimental study. The Womersley number is also important in determining the thickness of the boundary layer to see if entrance effects can be ignored.
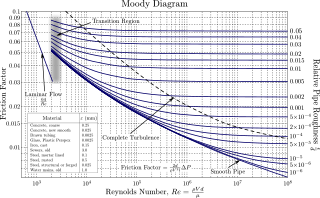
In engineering, the Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy–Weisbach friction factor fD, Reynolds number Re, and surface roughness for fully developed flow in a circular pipe. It can be used to predict pressure drop or flow rate down such a pipe.
In non ideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.
In physics, f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl (although ϕ was used rather than f for the name of the arbitrary function). It has become an active field of research following work by Alexei Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.
In fluid mechanics, dynamic similarity is the phenomenon that when there are two geometrically similar vessels with the same boundary conditions and the same Reynolds and Womersley numbers, then the fluid flows will be identical. This can be seen from inspection of the underlying Navier-Stokes equation, with geometrically similar bodies, equal Reynolds and Womersley Numbers the functions of velocity (u’,v’,w’) and pressure (P’) for any variation of flow.
In fluid dynamics, the Falkner–Skan boundary layer describes the steady two-dimensional laminar boundary layer that forms on a wedge, i.e. flows in which the plate is not parallel to the flow. It is also representative of flow on a flat plate with an imposed pressure gradient along the plate length, a situation often encountered in wind tunnel flow. It is a generalization of the flat plate Blasius boundary layer in which the pressure gradient along the plate is zero.
 | This article about a number is a stub. You can help Wikipedia by expanding it. |
