
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. It has become vital in the building of the Standard Model.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold. It is a local invariant of Riemannian metrics that measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is flat, i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
Linear elasticity is a mathematical model as to how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is

The Maxwell stress tensor is a symmetric second-order tensor in three dimensions that is used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.

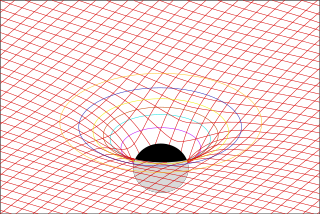
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.

In continuum mechanics, hydrostatic stress, also known as isotropic stress or volumetric stress, is a component of stress which contains uniaxial stresses, but not shear stresses. A specialized case of hydrostatic stress contains isotropic compressive stress, which changes only in volume, but not in shape. Pure hydrostatic stress can be experienced by a point in a fluid such as water. It is often used interchangeably with "mechanical pressure" and is also known as confining stress, particularly in the field of geomechanics.

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
Volume viscosity is a material property relevant for characterizing fluid flow. Common symbols are or . It has dimensions, and the corresponding SI unit is the pascal-second (Pa·s).
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
In mathematical physics, the Belinfante–Rosenfeld tensor is a modification of the stress–energy tensor that is constructed from the canonical stress–energy tensor and the spin current so as to be symmetric yet still conserved.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.



















