Marangoni number

Last updated November 24, 2022

The Marangoni number (Ma) is, as usually defined, the dimensionless number that compares the rate of transport due to Marangoni flows, with the rate of transport of diffusion. The Marangoni effect is flow of a liquid due to gradients in the surface tension of the liquid. Diffusion is of whatever is creating the gradient in the surface tension. Thus as the Marangoni number compares flow and diffusion timescales it is a type of Péclet number.

The Marangoni number is defined as:

\mathrm {Ma} ={\dfrac {\mbox{advective transport rate, due to surface tension gradient}}{\mbox{diffusive transport rate, of source of gradient}}}

A common example is surface tension gradients caused by temperature gradients.^[1] Then the relevant diffusion process is that of thermal energy (heat). Another is surface gradients caused by variations in the concentration of surfactants, where the diffusion is now that of surfactant molecules.

The number is named after Italian scientist Carlo Marangoni, although its use dates from the 1950s^[1]^[2] and it was neither discovered nor used by Carlo Marangoni.

The Marangoni number for a simple liquid of viscosity $\mu$ with a surface tension change $\Delta \gamma$ over a distance $L$ parallel to the surface, can be estimated as follows. Note that we assume that $L$ is the only length scale in the problem, which in practice implies that the liquid be at least $L$ deep. The transport rate is usually estimated using the equations of Stokes flow, where the fluid velocity is obtained by equating the stress gradient to the viscous dissipation. A surface tension is a force per unit length, so the resulting stress must scale as $\Delta \gamma /L$ , while the viscous stress scales as $\mu u/L$ , for $u$ the speed of the Marangoni flow. Equating the two we have a flow speed $u=\Delta \gamma /\mu$ . As Ma is a type of Péclet number, it is a velocity times a length, divided by a diffusion constant, $D$ , Here this is the diffusion constant of whatever is causing the surface tension difference. So,

\mathrm {Ma} ={\dfrac {uL}{D}}={\dfrac {\Delta \gamma L}{\mu D}}

Marangoni number due to thermal gradients

A common application is to a layer of liquid, such as water, when there is a temperature difference $\Delta T$ across this layer. This could be due to the liquid evaporating or being heated from below. There is a surface tension at the surface of a liquid that depends on temperature, typically as the temperature increases the surface tension decreases. Thus if due to a small fluctuation temperature, one part of the surface is hotter than another, there will be flow from the hotter part to the colder part, driven by this difference in surface tension, this flow is called the Marangoni effect. This flow will transport thermal energy, and the Marangoni number compares the rate at which thermal energy is transported by this flow to the rate at which thermal energy diffuses.

For a liquid layer of thickness $L$ , viscosity $\mu$ and thermal diffusivity $\alpha$ , with a surface tension $\gamma$ which changes with temperature at a rate $\partial \gamma /\partial T$ , the Marangoni number can be calculated using the following formula:^[3]

\mathrm {Ma} =-(\partial \gamma /\partial T).{\frac {L.\Delta T}{\mu .\alpha }}

When Ma is small thermal diffusion dominates and there is no flow, but for large Ma, flow (convection) occurs, driven by the gradients in the surface tension. This is called Bénard-Marangoni convection.

Related Research Articles

<span class="mw-page-title-main">Fick's laws of diffusion</span> Mathematical descriptions of molecular diffusion

Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, $D$ . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.

Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity. When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow.

In continuum mechanics, the Péclet number is a class of dimensionless numbers relevant in the study of transport phenomena in a continuum. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient. In the context of species or mass transfer, the Péclet number is the product of the Reynolds number and the Schmidt number. In the context of the thermal fluids, the thermal Péclet number is equivalent to the product of the Reynolds number and the Prandtl number.

The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:

In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.

In fluid mechanics, the Rayleigh number ( $Ra$ , after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 10⁶ to 10⁸.

Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its thermal conductivity, and is denoted $k$ .

<span class="mw-page-title-main">Heat transfer</span> Transport of thermal energy in physical systems

Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species, either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system.

<span class="mw-page-title-main">Boundary layer</span> Layer of fluid in the immediate vicinity of a bounding surface

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.

The Knudsen number (Kn) is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid. The number is named after Danish physicist Martin Knudsen (1871–1949).

Darcy's law is an equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference via the hydraulic conductivity.

There are two different Bejan numbers (Be) used in the scientific domains of thermodynamics and fluid mechanics. Bejan numbers are named after Adrian Bejan.

The Marangoni effect is the mass transfer along an interface between two phases due to a gradient of the surface tension. In the case of temperature dependence, this phenomenon may be called thermo-capillary convection.

In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.

The Herschel–Bulkley fluid is a generalized model of a non-Newtonian fluid, in which the strain experienced by the fluid is related to the stress in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress $. The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.$

<span class="mw-page-title-main">Diffusion</span> Transport of dissolved species from the highest to the lowest concentration region

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition.

Forced convection is type of heat transport in which fluid motion is generated by an external source like a. Heat transfer through porus media is very effective and efficiently. Forced convection heat transfer in a confined porous medium has been a subject of intensive studies during the last decades because of its wide applications.

The removal of heat from nuclear reactors is an essential step in the generation of energy from nuclear reactions. In nuclear engineering there are a number of empirical or semi-empirical relations used for quantifying the process of removing heat from a nuclear reactor core so that the reactor operates in the projected temperature interval that depends on the materials used in the construction of the reactor. The effectiveness of removal of heat from the reactor core depends on many factors, including the cooling agents used and the type of reactor. Common liquid coolants for nuclear reactors include: deionized water, heavy water, the lighter alkaline metals, lead or lead-based eutectic alloys like lead-bismuth, and NaK, a eutectic alloy of sodium and potassium. Gas cooled reactors operate with coolants like carbon dioxide, helium or nitrogen but some very low powered research reactors have even been air-cooled with Chicago Pile 1 relying on natural convection of the surrounding air to remove the negligible thermal power output. There is ongoing research into using supercritical fluids as reactor coolants but thus far neither the supercritical water reactor nor a reactor cooled with supercritical Carbon Dioxide nor any other kind of supercritical-fluid-cooled reactor has ever been built.

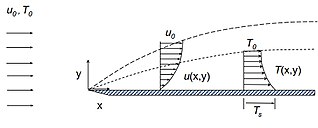
This page describes some parameters used to characterize the properties of the thermal boundary layer formed by a heated fluid moving along a heated wall. In many ways, the thermal boundary layer description parallels the velocity (momentum) boundary layer description first conceptualized by Ludwig Prandtl. Consider a fluid of uniform temperature $and velocity impinging onto a stationary plate uniformly heated to a temperature . Assume the flow and the plate are semi-infinite in the positive/negative direction perpendicular to the plane. As the fluid flows along the wall, the fluid at the wall surface satisfies a no-slip boundary condition and has zero velocity, but as you move away from the wall, the velocity of the flow asymptotically approaches the free stream velocity . The temperature at the solid wall is and gradually changes to as one moves toward the free stream of the fluid. It is impossible to define a sharp point at which the thermal boundary layer fluid or the velocity boundary layer fluid becomes the free stream, yet these layers have a well-defined characteristic thickness given by and . The parameters below provide a useful definition of this characteristic, measurable thickness for the thermal boundary layer. Also included in this boundary layer description are some parameters useful in describing the shape of the thermal boundary layer.$

References

1 2 Pearson, J. R. A. (1958). "On convection cells induced by surface tension". Journal of Fluid Mechanics. 4 (5): 489–500. Bibcode:1958JFM.....4..489P. doi:10.1017/S0022112058000616. ISSN 0022-1120. S2CID 123404447.
↑ Block, Myron J. (1956). "Surface Tension as the Cause of Bénard Cells and Surface Deformation in a Liquid Film". Nature. 178 (4534): 650–651. Bibcode:1956Natur.178..650B. doi:10.1038/178650a0. ISSN 0028-0836. S2CID 4273633.
↑ Pr. Steven Abbott. "Marangoni Number Calculator". stevenabbott.co.uk. Retrieved 2 March 2019.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 Pearson, J. R. A. (1958). "On convection cells induced by surface tension". Journal of Fluid Mechanics. 4 (5): 489–500. Bibcode:1958JFM.....4..489P. doi:10.1017/S0022112058000616. ISSN 0022-1120. S2CID 123404447.

[2] Block, Myron J. (1956). "Surface Tension as the Cause of Bénard Cells and Surface Deformation in a Liquid Film". Nature. 178 (4534): 650–651. Bibcode:1956Natur.178..650B. doi:10.1038/178650a0. ISSN 0028-0836. S2CID 4273633.

[3] Pr. Steven Abbott. "Marangoni Number Calculator". stevenabbott.co.uk. Retrieved 2 March 2019.

[1]

[2]

[3]