The speed of sound is the distance travelled per unit time by a sound wave as it propagates through an elastic medium. At 20 °C (68 °F), the speed of sound in air is about 343 meters per second, or a kilometre in 2.9 s or a mile in 4.7 s. It depends strongly on temperature, but also varies by several meters per second, depending on which gases exist in the medium through which a soundwave is propagating.

In thermodynamics and fluid mechanics, compressibility is a measure of the relative volume change of a fluid or solid as a response to a pressure change. In its simple form, the compressibility may be expressed as

In fluid dynamics, the Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. The equations represent Cauchy equations of conservation of mass (continuity), and balance of momentum and energy, and can be seen as particular Navier–Stokes equations with zero viscosity and zero thermal conductivity. In fact, Euler equations can be obtained by linearization of some more precise continuity equations like Navier–Stokes equations in a local equilibrium state given by a Maxwellian. The Euler equations can be applied to incompressible and to compressible flow – assuming the flow velocity is a solenoidal field, or using another appropriate energy equation respectively. Historically, only the incompressible equations have been derived by Euler. However, fluid dynamics literature often refers to the full set – including the energy equation – of the more general compressible equations together as "the Euler equations".
The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a shock wave or a combustion wave in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine and French engineer Pierre Henri Hugoniot.
The Knudsen number (Kn) is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid. The number is named after Danish physicist Martin Knudsen (1871–1949).
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.

The bulk modulus of a substance is a measure of how resistant to compression that substance is. It is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. Other moduli describe the material's response (strain) to other kinds of stress: the shear modulus describes the response to shear, and Young's modulus describes the response to linear stress. For a fluid, only the bulk modulus is meaningful. For a complex anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law.

An oblique shock wave, unlike a normal shock, is inclined with respect to the incident upstream flow direction. It will occur when a supersonic flow encounters a corner that effectively turns the flow into itself and compresses. The upstream streamlines are uniformly deflected after the shock wave. The most common way to produce an oblique shock wave is to place a wedge into supersonic, compressible flow. Similar to a normal shock wave, the oblique shock wave consists of a very thin region across which nearly discontinuous changes in the thermodynamic properties of a gas occur. While the upstream and downstream flow directions are unchanged across a normal shock, they are different for flow across an oblique shock wave.
Rayleigh flow refers to frictionless, non-Adiabatic flow through a constant area duct where the effect of heat addition or rejection is considered. Compressibility effects often come into consideration, although the Rayleigh flow model certainly also applies to incompressible flow. For this model, the duct area remains constant and no mass is added within the duct. Therefore, unlike Fanno flow, the stagnation temperature is a variable. The heat addition causes a decrease in stagnation pressure, which is known as the Rayleigh effect and is critical in the design of combustion systems. Heat addition will cause both supersonic and subsonic Mach numbers to approach Mach 1, resulting in choked flow. Conversely, heat rejection decreases a subsonic Mach number and increases a supersonic Mach number along the duct. It can be shown that for calorically perfect flows the maximum entropy occurs at M = 1. Rayleigh flow is named after John Strutt, 3rd Baron Rayleigh.
In fluid dynamics, stagnation pressure is the static pressure at a stagnation point in a fluid flow. At a stagnation point the fluid velocity is zero and all kinetic energy has been converted into pressure energy (isentropically). In an incompressible flow, stagnation pressure is equal to the sum of the free-stream dynamic pressure and free-stream static pressure.
The Euler number (Eu) is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop caused by a restriction and the kinetic energy per volume of the flow, and is used to characterize energy losses in the flow, where a perfect frictionless flow corresponds to an Euler number of 1. The inverse of the Euler number is referred to as the Ruark Number with the symbol Ru.
In fluid dynamics the Eötvös number (Eo), also called the Bond number (Bo), is a dimensionless number measuring the importance of gravitational forces compared to surface tension forces and is used to characterize the shape of bubbles or drops moving in a surrounding fluid. The two names commemorate the Hungarian physicist Loránd Eötvös (1848–1919) and the English physicist Wilfrid Noel Bond (1897–1937), respectively. The term Eötvös number is more frequently used in Europe, while Bond number is commonly used in other parts of the world.
Dynamic pressure is the increase in a moving fluid's pressure over its static value due to motion. In incompressible fluid dynamics, it is indicated as , or Q, defined by:
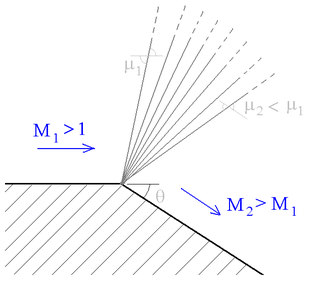
A supersonic expansion fan, technically known as Prandtl–Meyer expansion fan, is a centred expansion process that occurs when a supersonic flow turns around a convex corner. The fan consists of an infinite number of Mach waves, diverging from a sharp corner. When a flow turns around a smooth and circular corner, these waves can be extended backwards to meet at a point.
In fluid dynamics, a moving shock is a shock wave that is travelling through a fluid medium with a velocity relative to the velocity of the fluid already making up the medium. As such, the normal shock relations require modification to calculate the properties before and after the moving shock. A knowledge of moving shocks is important for studying the phenomena surrounding detonation, among other applications.
Fanno flow is the adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow is assumed to be steady and one-dimensional, and no mass is added within the duct. The Fanno flow model is considered an irreversible process due to viscous effects. The viscous friction causes the flow properties to change along the duct. The frictional effect is modeled as a shear stress at the wall acting on the fluid with uniform properties over any cross section of the duct.
In compressible fluid dynamics, impact pressure is the difference between total pressure and static pressure. In aerodynamics notation, this quantity is denoted as or .
Isentropic nozzle flow describes the movement of a gas or fluid through a narrowing opening without an increase or decrease in entropy.













