A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that use mechanical advantage to multiply force. Usually the term refers to the six classical simple machines that were defined by Renaissance scientists:

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

An inclined plane, also known as a ramp, is a flat supporting surface tilted at an angle from the vertical direction, with one end higher than the other, used as an aid for raising or lowering a load. The inclined plane is one of the six classical simple machines defined by Renaissance scientists. Inclined planes are used to move heavy loads over vertical obstacles. Examples vary from a ramp used to load goods into a truck, to a person walking up a pedestrian ramp, to an automobile or railroad train climbing a grade.

In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.

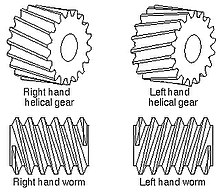
A gear is a rotating circular machine part having cut teeth or, in the case of a cogwheel or gearwheel, inserted teeth, which mesh with another (compatible) toothed part to transmit rotational power. While doing so, they can change the torque and rotational speed being transmitted and also change the rotational axis of the power being transmitted. The teeth on the two meshing gears all have the same shape.
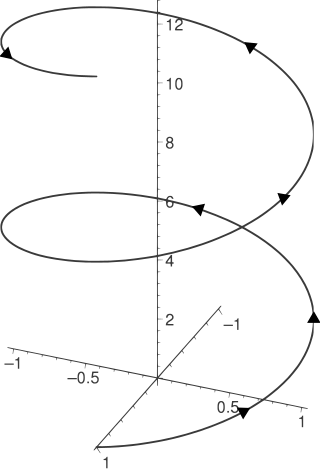
A helix is a shape like a corkscrew. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word helix comes from the Greek word ἕλιξ, "twisted, curved". A "filled-in" helix – for example, a "spiral" (helical) ramp – is a surface called a helicoid.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

The great-circle distance, orthodromic distance, or spherical distance is the distance along a great circle.
Blade element theory (BET) is a mathematical process originally designed by William Froude (1878), David W. Taylor (1893) and Stefan Drzewiecki (1885) to determine the behavior of propellers. It involves breaking a blade down into several small parts then determining the forces on each of these small blade elements. These forces are then integrated along the entire blade and over one rotor revolution in order to obtain the forces and moments produced by the entire propeller or rotor. One of the key difficulties lies in modelling the induced velocity on the rotor disk. Because of this the blade element theory is often combined with momentum theory to provide additional relationships necessary to describe the induced velocity on the rotor disk, producing blade element momentum theory. At the most basic level of approximation a uniform induced velocity on the disk is assumed:
A nonholonomic system in physics and mathematics is a physical system whose state depends on the path taken in order to achieve it. Such a system is described by a set of parameters subject to differential constraints and non-linear constraints, such that when the system evolves along a path in its parameter space but finally returns to the original set of parameter values at the start of the path, the system itself may not have returned to its original state. Nonholonomic mechanics is autonomous division of Newtonian mechanics.

In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half an angle is the stereographic projection of the circle through the point at angle onto the line through the angles . Among these formulas are the following:
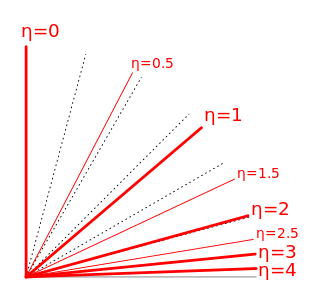
In experimental particle physics, pseudorapidity, , is a commonly used spatial coordinate describing the angle of a particle relative to the beam axis. It is defined as

A leadscrew, also known as a power screw or translation screw, is a screw used as a linkage in a machine, to translate turning motion into linear motion. Because of the large area of sliding contact between their male and female members, screw threads have larger frictional energy losses compared to other linkages. They are not typically used to carry high power, but more for intermittent use in low power actuator and positioner mechanisms. Leadscrews are commonly used in linear actuators, machine slides, vises, presses, and jacks. Leadscrews are a common component in electric linear actuators.

A ball screw is a mechanical linear actuator that translates rotational motion to linear motion with little friction. A threaded shaft provides a helical raceway for ball bearings which act as a precision screw. As well as being able to apply or withstand high thrust loads, they can do so with minimum internal friction. They are made to close tolerances and are therefore suitable for use in situations in which high precision is necessary. The ball assembly acts as the nut while the threaded shaft is the screw.

A screw is a mechanism that converts rotational motion to linear motion, and a torque to a linear force. It is one of the six classical simple machines. The most common form consists of a cylindrical shaft with helical grooves or ridges called threads around the outside. The screw passes through a hole in another object or medium, with threads on the inside of the hole that mesh with the screw's threads. When the shaft of the screw is rotated relative to the stationary threads, the screw moves along its axis relative to the medium surrounding it; for example rotating a wood screw forces it into wood. In screw mechanisms, either the screw shaft can rotate through a threaded hole in a stationary object, or a threaded collar such as a nut can rotate around a stationary screw shaft. Geometrically, a screw can be viewed as a narrow inclined plane wrapped around a cylinder.
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of right triangles. The proofs given in this article use this definition, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

Lateral earth pressure is the pressure that soil exerts in the horizontal direction. The lateral earth pressure is important because it affects the consolidation behavior and strength of the soil and because it is considered in the design of geotechnical engineering structures such as retaining walls, basements, tunnels, deep foundations and braced excavations.
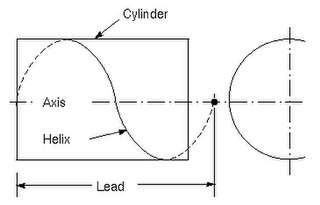
Lead is the axial advance of a helix or screw during one complete turn (360°) The lead for a screw thread is the axial travel for a single revolution.
Propeller theory is the science governing the design of efficient propellers. A propeller is the most common propulsor on ships, and on small aircraft.