The Kochsnowflake is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Curve Without Tangents, Constructible from Elementary Geometry" by the Swedish mathematician Helge von Koch.

In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.

A helix is a shape like a cylindrical coil spring or the thread of a machine screw. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word helix comes from the Greek word ἕλιξ, "twisted, curved". A "filled-in" helix – for example, a "spiral" (helical) ramp – is a surface called a helicoid.
DNA topoisomerases are enzymes that catalyze changes in the topological state of DNA, interconverting relaxed and supercoiled forms, linked (catenated) and unlinked species, and knotted and unknotted DNA. Topological issues in DNA arise due to the intertwined nature of its double-helical structure, which, for example, can lead to overwinding of the DNA duplex during DNA replication and transcription. If left unchanged, this torsion would eventually stop the DNA or RNA polymerases involved in these processes from continuing along the DNA helix. A second topological challenge results from the linking or tangling of DNA during replication. Left unresolved, links between replicated DNA will impede cell division. The DNA topoisomerases prevent and correct these types of topological problems. They do this by binding to DNA and cutting the sugar-phosphate backbone of either one or both of the DNA strands. This transient break allows the DNA to be untangled or unwound, and, at the end of these processes, the DNA backbone is resealed. Since the overall chemical composition and connectivity of the DNA do not change, the DNA substrate and product are chemical isomers, differing only in their topology.
In mathematics, a modular equation is an algebraic equation satisfied by moduli, in the sense of moduli problems. That is, given a number of functions on a moduli space, a modular equation is an equation holding between them, or in other words an identity for moduli.
In knot theory, there are several competing notions of the quantity writhe, or . In one sense, it is purely a property of an oriented link diagram and assumes integer values. In another sense, it is a quantity that describes the amount of "coiling" of a mathematical knot in three-dimensional space and assumes real numbers as values. In both cases, writhe is a geometric quantity, meaning that while deforming a curve in such a way that does not change its topology, one may still change its writhe.

In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.

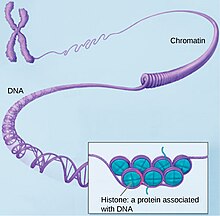
In molecular biology, the term double helix refers to the structure formed by double-stranded molecules of nucleic acids such as DNA. The double helical structure of a nucleic acid complex arises as a consequence of its secondary structure, and is a fundamental component in determining its tertiary structure. The structure was discovered by Maurice Wilkins, Rosalind Franklin, her student Raymond Gosling, James Watson, and Francis Crick, while the term "double helix" entered popular culture with the 1968 publication of Watson's The Double Helix: A Personal Account of the Discovery of the Structure of DNA.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas.

DNA supercoiling refers to the amount of twist in a particular DNA strand, which determines the amount of strain on it. A given strand may be "positively supercoiled" or "negatively supercoiled". The amount of a strand's supercoiling affects a number of biological processes, such as compacting DNA and regulating access to the genetic code. Certain enzymes, such as topoisomerases, change the amount of DNA supercoiling to facilitate functions such as DNA replication and transcription. The amount of supercoiling in a given strand is described by a mathematical formula that compares it to a reference state known as "relaxed B-form" DNA.
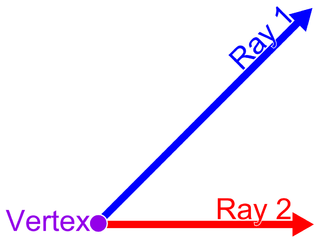
In geometry, a vertex is a point where two or more curves, lines, or edges meet or intersect. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedron are vertices.
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.

In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.

Molecular models of DNA structures are representations of the molecular geometry and topology of deoxyribonucleic acid (DNA) molecules using one of several means, with the aim of simplifying and presenting the essential, physical and chemical, properties of DNA molecular structures either in vivo or in vitro. These representations include closely packed spheres made of plastic, metal wires for skeletal models, graphic computations and animations by computers, artistic rendering. Computer molecular models also allow animations and molecular dynamics simulations that are very important for understanding how DNA functions in vivo.

Nucleic acid structure refers to the structure of nucleic acids such as DNA and RNA. Chemically speaking, DNA and RNA are very similar. Nucleic acid structure is often divided into four different levels: primary, secondary, tertiary, and quaternary.
In differential geometry, a ribbon is the combination of a smooth space curve and its corresponding normal vector. More formally, a ribbon denoted by includes a curve given by a three-dimensional vector , depending continuously on the curve arc-length , and a unit vector perpendicular to at each point. Ribbons have seen particular application as regards DNA.
In differential geometry, the twist of a ribbon is its rate of axial rotation. Let a ribbon be composed of a space curve, , where is the arc length of , and the a unit normal vector, perpendicular at each point to . Since the ribbon has edges and , the twist measures the average winding of the edge curve around and along the axial curve . According to Love (1944) twist is defined by

The Minkowski sausage or Minkowski curve is a fractal first proposed by and named for Hermann Minkowski as well as its casual resemblance to a sausage or sausage links. The initiator is a line segment and the generator is a broken line of eight parts one fourth the length.

Gheorghe Călugăreanu was a Romanian mathematician, professor at Babeș-Bolyai University, and full member of the Romanian Academy.