This is a list of Wikipedia articles about curves used in different fields: mathematics (including geometry, statistics, and applied mathematics), physics, engineering, economics, medicine, biology, psychology, ecology, etc.
Rational curves are subdivided according to the degree of the polynomial.
Plane curves of degree 2 are known as conics or conic sections and include
Cubic plane curves include
Quartic plane curves include
See also List of fractals by Hausdorff dimension.
| Curves |  | ||
|---|---|---|---|
| Helices |
| ||
| Spirals | |||
In geometry, a limaçon or limacon, also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp.
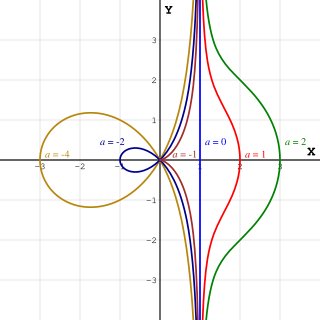
In algebraic geometry, the conchoids of de Sluze are a family of plane curves studied in 1662 by Walloon mathematician René François Walter, baron de Sluze.
In geometry, a conchoid is a curve derived from a fixed point O, another curve, and a length d. It was invented by the ancient Greek mathematician Nicomedes.
In geometry, a cissoid is a plane curve generated from two given curves C1, C2 and a point O. Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.
In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points (foci) is constant. This may be contrasted with an ellipse, for which the sum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.
In geometry, a hippopede is a plane curve determined by an equation of the form
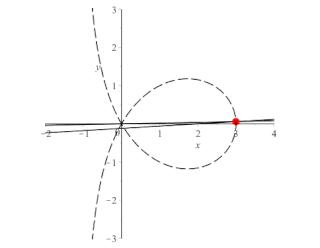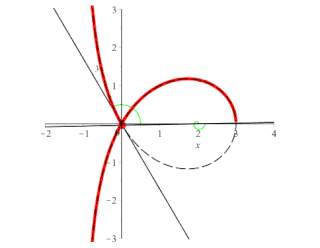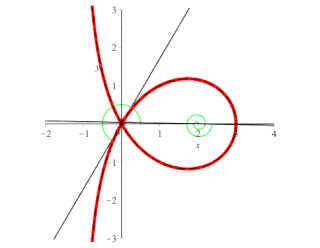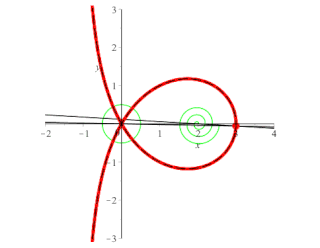
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742.
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle with ruler and compass and this curve as an additional tool. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of construction. There is a variety of such curves and the methods used to construct an angle trisector differ according to the curve. Examples include:
In algebraic geometry, a lemniscate is any of several figure-eight or ∞-shaped curves. The word comes from the Latin lēmniscātus meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbon", or which alternatively may refer to the wool from which the ribbons were made.
Perseus was an ancient Greek geometer, who invented the concept of spiric sections, in analogy to the conic sections studied by Apollonius of Perga.
In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.
This is a gallery of curves used in mathematics, by Wikipedia page. See also list of curves.
In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates
In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F(x, y) = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2. More precisely, if F = Fn + Fn−1 + ... + F1 + F0, where each Fi is homogeneous of degree i, then the curve F(x, y) = 0 is circular if and only if Fn is divisible by x2 + y2.
The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.
In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of some defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci – in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane is called an n–ellipse and can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, where one circle is inside the other, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates, the equation y = x2 represents a parabola. The generalized equation y = xr, for r ≠ 0 and r ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applications in approximation theory and optimization theory.