Algebraic curves
Rational curves
Degree 1
Degree 2
Degree 3
Degree 4
- Quadrifolium (2-rose)
Degree 5
Degree 6
- Atriphtaloid
This is a gallery of curves used in mathematics, by Wikipedia page. See also list of curves.

Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometrical problems. Classically, it studies zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects.

A Bézier curve is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation. Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

In geometry, a limaçon or limacon, also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp.

In mathematics, a cuspidal cubic or semicubical parabola is an algebraic plane curve that has an implicit equation of the form
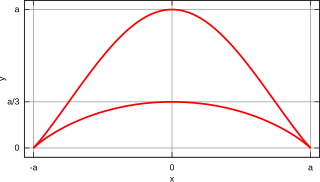
In geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equation
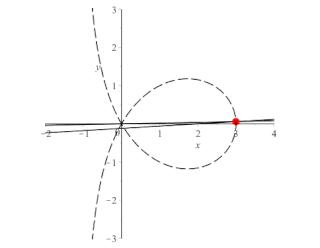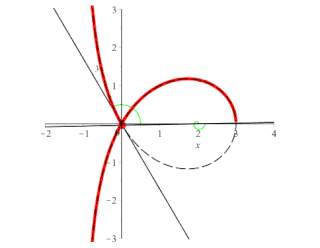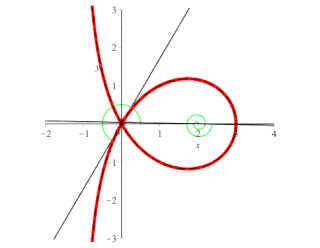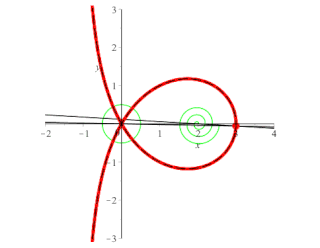
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742.
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle with ruler and compass and this curve as an additional tool. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of construction. There is a variety of such curves and the methods used to construct an angle trisector differ according to the curve. Examples include:

A transition curve is a spiral-shaped length of highway or railroad track that is used between sections having different profiles and radii, such as between straightaways (tangents) and curves, or between two different curves.

In algebraic geometry, a lemniscate is any of several figure-eight or ∞-shaped curves. The word comes from the Latin lēmniscātus, meaning "decorated with ribbons", from the Greek λημνίσκος (lēmnískos), meaning "ribbon", or which alternatively may refer to the wool from which the ribbons were made.

In mathematics, a polynomial lemniscate or polynomial level curve is a plane algebraic curve of degree 2n, constructed from a polynomial p with complex coefficients of degree n.

In algebraic geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation

In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.

In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F(x, y) = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2. More precisely, if F = Fn + Fn−1 + ... + F1 + F0, where each Fi is homogeneous of degree i, then the curve F(x, y) = 0 is circular if and only if Fn is divisible by x2 + y2.
In 1876 Alfred B. Kempe published his article On a General Method of describing Plane Curves of the nth degree by Linkwork, which showed that for an arbitrary algebraic plane curve a linkage can be constructed that draws the curve. This direct connection between linkages and algebraic curves has been named Kempe's universality theorem that any bounded subset of an algebraic curve may be traced out by the motion of one of the joints in a suitably chosen linkage. Kempe's proof was flawed and the first complete proof was provided in 2002 based on his ideas.