Minimal surfaces

This is a list of surfaces in mathematics. They are divided into minimal surfaces, ruled surfaces, non-orientable surfaces, quadrics, pseudospherical surfaces, algebraic surfaces, and other types of surfaces.

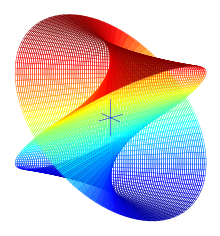



| | This section is empty. You can help by adding to it. (November 2014) |

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.

In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane.

In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero, but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function has a critical point at that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the -direction.

The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known.
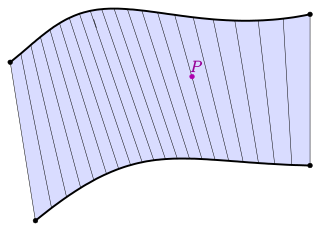
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

In structural engineering, a tensile structure is a construction of elements carrying only tension and no compression or bending. The term tensile should not be confused with tensegrity, which is a structural form with both tension and compression elements. Tensile structures are the most common type of thin-shell structures.
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola, to hyperbole, or to hyperbolic geometry.

In three-dimensional geometry, skew lines are two lines that do not intersect and are not parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions. Two lines are skew if and only if they are not coplanar.

In mathematics, a developable surface is a smooth surface with zero Gaussian curvature. That is, it is a surface that can be flattened onto a plane without distortion. Conversely, it is a surface which can be made by transforming a plane. In three dimensions all developable surfaces are ruled surfaces. There are developable surfaces in four-dimensional space which are not ruled.

Hyperboloid structures are architectural structures designed using a hyperboloid in one sheet. Often these are tall structures, such as towers, where the hyperboloid geometry's structural strength is used to support an object high above the ground. Hyperboloid geometry is often used for decorative effect as well as structural economy. The first hyperboloid structures were built by Russian engineer Vladimir Shukhov (1853–1939), including the Shukhov Tower in Polibino, Dankovsky District, Lipetsk Oblast, Russia.

jrMan renderer is an open-source version of the Reyes rendering algorithm used by Pixar's PhotoRealistic RenderMan, implemented in Java by Gerardo Horvilleur, Jorge Vargas, Elmer Garduno and Alessandro Falappa.
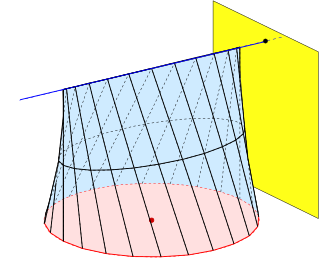
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:
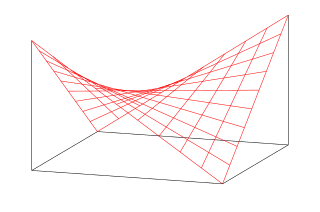
A saddle roof is a roof form which follows a convex curve about one axis and a concave curve about the other. The hyperbolic paraboloid form has been used for roofs at various times since it is easily constructed from straight sections of lumber, steel, or other conventional materials. The term is used because the form resembles the shape of a saddle.