A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In the theory of Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .
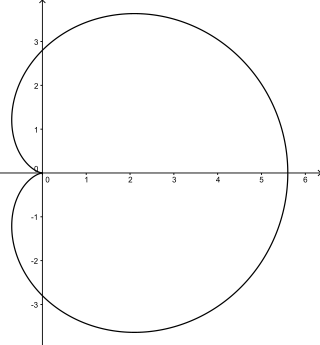
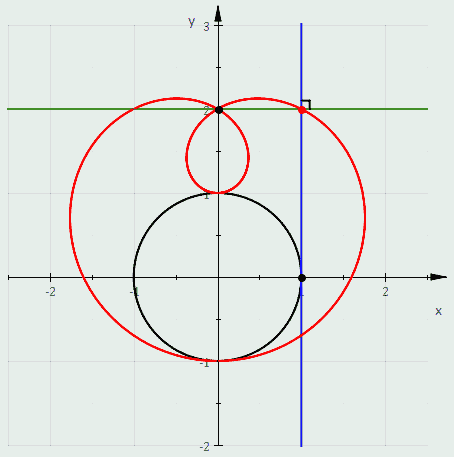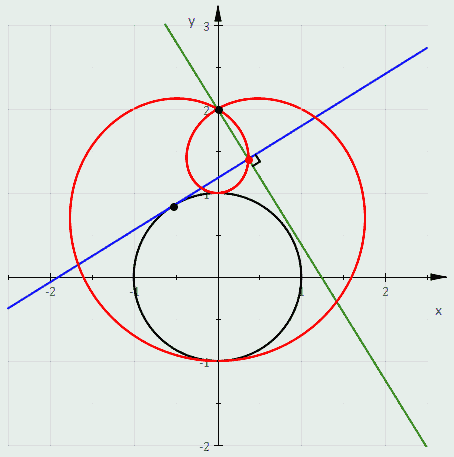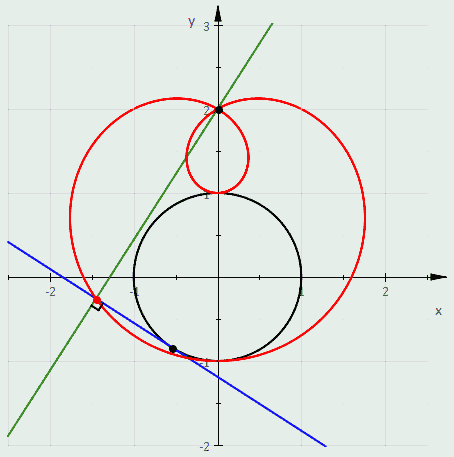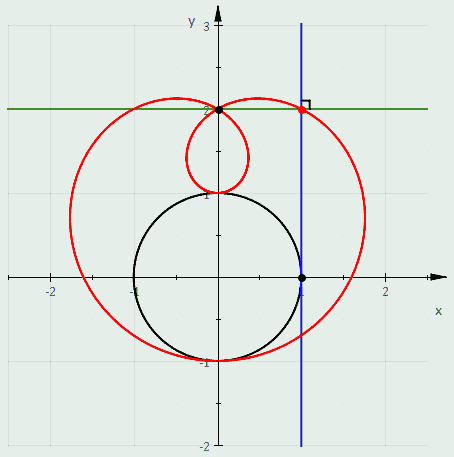
In geometry, a cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.
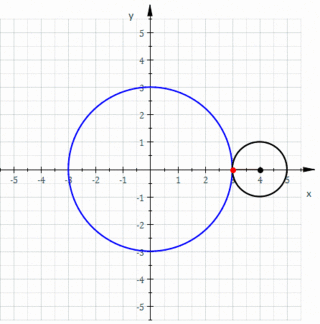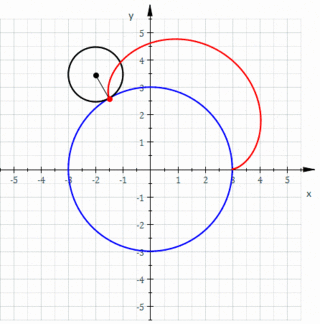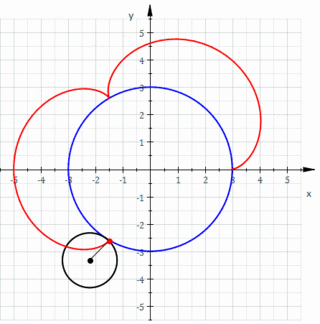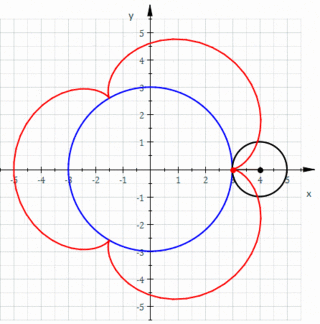
In geometry, an epicycloid(also called hypercycloid) is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an epicycle—which rolls without slipping around a fixed circle. It is a particular kind of roulette.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.

In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the point on the circle opposite to the point of tangency. In fact, the curve family of cissoids is named for this example and some authors refer to it simply as the cissoid. It has a single cusp at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote. It is a member of the conchoid of de Sluze family of curves and in form it resembles a tractrix.

In mathematics, an involute is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve.

In geometry, a nephroid is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger one by a factor of one-half.

In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

In geometry, a cissoid ( is a plane curve generated from two given curves C1, C2 and a point O. Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.

In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half an angle is the stereographic projection of the circle onto a line. Among these formulas are the following:

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p. Its center lies on the inner normal line, and its curvature defines the curvature of the given curve at that point. This circle, which is the one among all tangent circles at the given point that approaches the curve most tightly, was named circulus osculans by Leibniz.

In geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.

In mathematics, Watt's curve is a tricircular plane algebraic curve of degree six. It is generated by two circles of radius b with centers distance 2a apart. A line segment of length 2c attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine.
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of right triangles. The proofs given in this article use this definition, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to

In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.
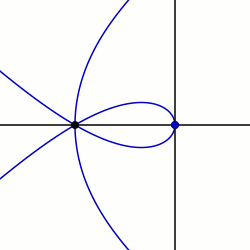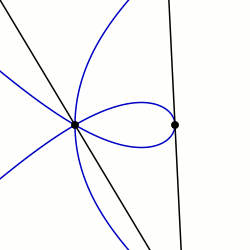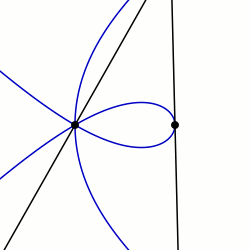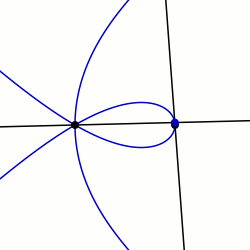
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin, which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
For a plane curve C and a given fixed point O, the pedal equation of the curve is a relation between r and p where r is the distance from O to a point on C and p is the perpendicular distance from O to the tangent line to C at the point. The point O is called the pedal point and the values r and p are sometimes called the pedal coordinates of a point relative to the curve and the pedal point. It is also useful to measure the distance of O to the normal even though it is not an independent quantity and it relates to as .