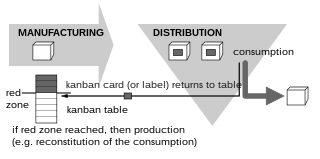
Kanban is a scheduling system for lean manufacturing. Taiichi Ohno, an industrial engineer at Toyota, developed kanban to improve manufacturing efficiency. The system takes its name from the cards that track production within a factory. Kanban is also known as the Toyota nameplate system in the automotive industry.
In the field of mathematical optimization, stochastic programming is a framework for modeling optimization problems that involve uncertainty. A stochastic program is an optimization problem in which some or all problem parameters are uncertain, but follow known probability distributions. This framework contrasts with deterministic optimization, in which all problem parameters are assumed to be known exactly. The goal of stochastic programming is to find a decision which both optimizes some criteria chosen by the decision maker, and appropriately accounts for the uncertainty of the problem parameters. Because many real-world decisions involve uncertainty, stochastic programming has found applications in a broad range of areas ranging from finance to transportation to energy optimization.
In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, S. Watanabe, I. Shigekawa, and so on finally completed the foundations.
Economic Order Quantity (EOQ), also known as Financial Purchase Quantity or Economic Buying Quantity, is the order quantity that minimizes the total holding costs and ordering costs in inventory management. It is one of the oldest classical production scheduling models. The model was developed by Ford W. Harris in 1913, but R. H. Wilson, a consultant who applied it extensively, and K. Andler are given credit for their in-depth analysis.
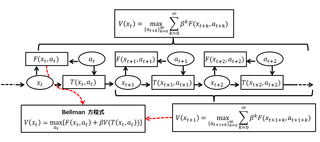
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices, random growth models or physical systems that are subjected to thermal fluctuations.
Service level measures the performance of a system. Certain goals are defined and the service level gives the percentage to which those goals should be achieved. Fill rate is different from service level.
Safety stock is a term used by logisticians to describe a level of extra stock that is maintained to mitigate risk of stockouts caused by uncertainties in supply and demand. Adequate safety stock levels permit business operations to proceed according to their plans. Safety stock is held when uncertainty exists in demand, supply, or manufacturing yield, and serves as an insurance against stockouts.
Inventory control or stock control can be broadly defined as "the activity of checking a shop's stock". It is the process of ensuring that the right amount of supply is available within a business. However, a more focused definition takes into account the more science-based, methodical practice of not only verifying a business's inventory but also maximising the amount of profit from the least amount of inventory investment without affecting customer satisfaction. Other facets of inventory control include forecasting future demand, supply chain management, production control, financial flexibility, purchasing data, loss prevention and turnover, and customer satisfaction.
The economic lot scheduling problem (ELSP) is a problem in operations management and inventory theory that has been studied by many researchers for more than 50 years. The term was first used in 1958 by professor Jack D. Rogers of Berkeley, who extended the economic order quantity model to the case where there are several products to be produced on the same machine, so that one must decide both the lot size for each product and when each lot should be produced. The method illustrated by Jack D. Rogers draws on a 1956 paper from Welch, W. Evert. The ELSP is a mathematical model of a common issue for almost any company or industry: planning what to manufacture, when to manufacture and how much to manufacture.
The newsvendormodel is a mathematical model in operations management and applied economics used to determine optimal inventory levels. It is (typically) characterized by fixed prices and uncertain demand for a perishable product. If the inventory level is , each unit of demand above is lost in potential sales. This model is also known as the newsvendor problem or newsboy problem by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day.
Merton's portfolio problem is a problem in continuous-time finance and in particular intertemporal portfolio choice. An investor must choose how much to consume and must allocate their wealth between stocks and a risk-free asset so as to maximize expected utility. The problem was formulated and solved by Robert C. Merton in 1969 both for finite lifetimes and for the infinite case. Research has continued to extend and generalize the model to include factors like transaction costs and bankruptcy.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
Robust optimization is a field of mathematical optimization theory that deals with optimization problems in which a certain measure of robustness is sought against uncertainty that can be represented as deterministic variability in the value of the parameters of the problem itself and/or its solution. It is related to, but often distinguished from, probabilistic optimization methods such as chance-constrained optimization.
The dynamic lot-size model in inventory theory, is a generalization of the economic order quantity model that takes into account that demand for the product varies over time. The model was introduced by Harvey M. Wagner and Thomson M. Whitin in 1958.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/c queue represents the queue length in a system having c servers, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. The model is an extension of the M/D/1 queue which has only a single server.
The base stock model is a statistical model in inventory theory. In this model inventory is refilled one unit at a time and demand is random. If there is only one replenishment, then the problem can be solved with the newsvendor model.
Supersymmetric theory of stochastic dynamics or stochastics (STS) is an exact theory of stochastic (partial) differential equations (SDEs), the class of mathematical models with the widest applicability covering, in particular, all continuous time dynamical systems, with and without noise. The main utility of the theory from the physical point of view is a rigorous theoretical explanation of the ubiquitous spontaneous long-range dynamical behavior that manifests itself across disciplines via such phenomena as 1/f, flicker, and crackling noises and the power-law statistics, or Zipf's law, of instantonic processes like earthquakes and neuroavalanches. From the mathematical point of view, STS is interesting because it bridges the two major parts of mathematical physics – the dynamical systems theory and topological field theories. Besides these and related disciplines such as algebraic topology and supersymmetric field theories, STS is also connected with the traditional theory of stochastic differential equations and the theory of pseudo-Hermitian operators.
The (Q,r) model is a class of models in inventory theory. A general (Q,r) model can be extended from both the EOQ model and the base stock model
K-convexity in Rn is a mathematical concept.












