In mathematics, the limiting amplitude principle is a concept from operator theory and scattering theory used for choosing a particular solution to the Helmholtz equation. The choice is made by considering a particular time-dependent problem of the forced oscillations due to the action of a periodic force. The principle was introduced by Andrey Nikolayevich Tikhonov and Alexander Andreevich Samarskii. [1] It is closely related to the limiting absorption principle (1905) and the Sommerfeld radiation condition (1912). The terminology -- both the limiting absorption principle and the limiting amplitude principle -- was introduced by Aleksei Sveshnikov. [2]
To find which solution to the Helmholz equation with nonzero right-hand side
with some fixed , corresponds to the outgoing waves, one considers the wave equation with the source term,
with zero initial data . A particular solution to the Helmholtz equation corresponding to outgoing waves is obtained as the limit
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a traveling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a wave equation or a one-way wave equation for single wave propagation in a defined direction.
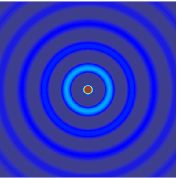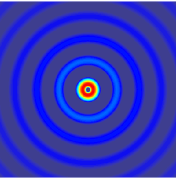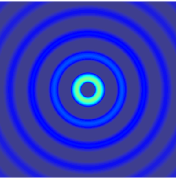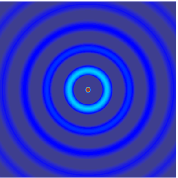
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics. A single wave propagating in a pre-defined direction can also be described with the one-way wave equation.
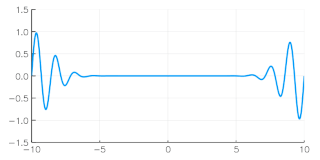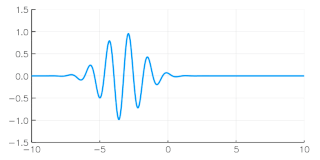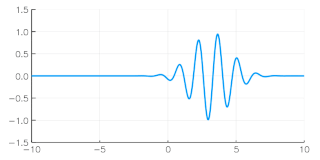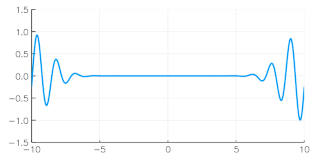
In physics, a wave packet is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear differential equations with spatially varying coefficients. It is typically used for a semiclassical calculation in quantum mechanics in which the wavefunction is recast as an exponential function, semiclassically expanded, and then either the amplitude or the phase is taken to be changing slowly.
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation
In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.
In mathematics, and more specifically in partial differential equations, Duhamel's principle is a general method for obtaining solutions to inhomogeneous linear evolution equations like the heat equation, wave equation, and vibrating plate equation. It is named after Jean-Marie Duhamel who first applied the principle to the inhomogeneous heat equation that models, for instance, the distribution of heat in a thin plate which is heated from beneath. For linear evolution equations without spatial dependency, such as a harmonic oscillator, Duhamel's principle reduces to the method of variation of parameters technique for solving linear inhomogeneous ordinary differential equations. It is also an indispensable tool in the study of nonlinear partial differential equations such as the Navier–Stokes equations and nonlinear Schrödinger equation where one treats the nonlinearity as an inhomogeneity.
In mathematics, the Sommerfeld radiation condition is a concept from theory of differential equations and scattering theory used for choosing a particular solution to the Helmholtz equation. It was introduced by Arnold Sommerfeld in 1912 and is closely related to the limiting absorption principle (1905) and the limiting amplitude principle (1948).
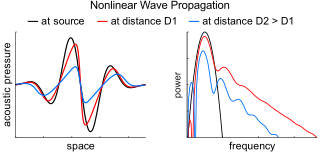
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.
In mathematics, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equations can arise as the Euler–Lagrange equations for some Lagrangian function.
In applied mathematics, discontinuous Galerkin methods form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics.
The Benjamin–Bona–Mahony equation is the partial differential equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
In mathematical physics and the theory of partial differential equations, the solitary wave solution of the form is said to be orbitally stable if any solution with the initial data sufficiently close to forever remains in a given small neighborhood of the trajectory of .
Derrick's theorem is an argument by physicist G.H. Derrick which shows that stationary localized solutions to a nonlinear wave equation or nonlinear Klein–Gordon equation in spatial dimensions three and higher are unstable.
In functional analysis, the Fréchet–Kolmogorov theorem gives a necessary and sufficient condition for a set of functions to be relatively compact in an Lp space. It can be thought of as an Lp version of the Arzelà–Ascoli theorem, from which it can be deduced. The theorem is named after Maurice René Fréchet and Andrey Kolmogorov.
The theory of causal fermion systems is an approach to describe fundamental physics. It provides a unification of the weak, the strong and the electromagnetic forces with gravity at the level of classical field theory. Moreover, it gives quantum mechanics as a limiting case and has revealed close connections to quantum field theory. Therefore, it is a candidate for a unified physical theory. Instead of introducing physical objects on a preexisting spacetime manifold, the general concept is to derive spacetime as well as all the objects therein as secondary objects from the structures of an underlying causal fermion system. This concept also makes it possible to generalize notions of differential geometry to the non-smooth setting. In particular, one can describe situations when spacetime no longer has a manifold structure on the microscopic scale. As a result, the theory of causal fermion systems is a proposal for quantum geometry and an approach to quantum gravity.
The Leray projection, named after Jean Leray, is a linear operator used in the theory of partial differential equations, specifically in the fields of fluid dynamics. Informally, it can be seen as the projection on the divergence-free vector fields. It is used in particular to eliminate both the pressure term and the divergence-free term in the Stokes equations and Navier–Stokes equations.
In mathematics, the limiting absorption principle (LAP) is a concept from operator theory and scattering theory that consists of choosing the "correct" resolvent of a linear operator at the essential spectrum based on the behavior of the resolvent near the essential spectrum. The term is often used to indicate that the resolvent, when considered not in the original space, but in certain weighted spaces, has a limit as the spectral parameter approaches the essential spectrum. This concept developed from the idea of introducing complex parameter into the Helmholtz equation for selecting a particular solution. This idea is credited to Vladimir Ignatowski, who was considering the propagation and absorption of the electromagnetic waves in a wire. It is closely related to the Sommerfeld radiation condition and the limiting amplitude principle (1948). The terminology – both the limiting absorption principle and the limiting amplitude principle – was introduced by Aleksei Sveshnikov.
{{cite journal}}: CS1 maint: multiple names: authors list (link)  | This mathematics-related article is a stub. You can help Wikipedia by expanding it. |
 | This scattering–related article is a stub. You can help Wikipedia by expanding it. |