Randolph diagram

"R-diagram" redirects here. For the H–R diagram, see Hertzsprung–Russell diagram.

Randolph diagram that represents the logical statement ${\displaystyle P\lor Q}$ (disjunction).

A Randolph diagram (R-diagram) is a simple way to visualize logical expressions and combinations of sets. Randolph diagrams were created by mathematician John F. Randolph in 1965, during his tenure at the University of Arkansas.

Overview

Randolph diagrams can be interpreted most easily by defining each line as belonging to or relating to one logical statement or set. Any dot above the line indicates truth or inclusion and below the line indicates falsity or exclusion. Using this system, one can represent any combination of sets or logical statements using intersecting lines.

Though Venn diagrams are more commonly used to represent combinations of sets, Randolph diagrams have the advantage of being able to cleanly represent combinations of more than 3 sets. Venn diagrams require either extension into higher spatial dimensions or the use of more complicated shapes while Randolph diagrams evenly subdivide for every additional set. ^[1] Here is a comparison between a Venn diagram and R-diagram for 5 sets of logical statements:

History

In his introductory paper on the subject, Cross-Examining Propositional Calculus and Set Operations, ^[2] Randolph mentions that the first use of crosses and dots to represent logical relationships was introduced by W. S. McCulloch, a neurophysiologist and Randolph's contemporary. Randolph modified McCulloch's system with a new way of representing combinations and relationships of more than two logical statements or sets, namely subdividing each section of the R-diagram with a new diagonal line for each new element introduced. Randolph's paper suggests that his original notion was to use R-diagrams to represent logical relationships, and then expanded the idea to be applied to set theory as well. Throughout the paper, R-diagrams are used in conjunction with normal logical and set binary operation symbols.

Application to logic theory

See also: Mathematical logic

When applying R-diagrams to logic theory, logical statements p, q, and r can each become a line or multiple lines to visually display the validity of each element in a larger statement. Generally, p is thought to be represented by an upward sloping line (/) while q is represented by a downward sloping line (\). A dot in the diagram above a slanting line indicates truth for that statement; likewise, a dot below indicates falsity. The R-diagrams for p and q are shown below, respectively:

For more than two statements, the four spaces formed by the intersection of lines p and q must be subdivided into more lines. In the case of r, a single upward sloping line (/) is added in each of the four spaces. The R-diagram for r is shown below:

This method can be extended for any number of truth values:

, etc.

R-diagrams are primarily used to represent logical expressions. Given a logical proposition, R-diagrams are able to display the outcome of every possible true/false variation of each element, creating an alternative way to represent a truth table.

Truth table

#	p	q	r
1	T	T	T
2	T	T	F
3	T	F	T
4	T	F	F
5	F	T	T
6	F	T	F
7	F	F	T
8	F	F	F

All the basic logical operations, or connectives, can be expressed using an R-diagrams as a more easily readable alternative to a truth table, as is shown in the table below:

Basic logical operations

Name	Symbols	R-diagram	Truth table
Negation (not)	¬ , ~		p ¬p T F F T
Conjunction (and)	& , ∧		p q p ∧ q T T T T F F F T F F F F
Disjunction (or)	∨		p q p ∨ q T T T T F T F T T F F F
Material implication (if...then)	${\displaystyle \rightarrow }$ , ${\displaystyle \Rightarrow }$, ${\displaystyle \supset }$		p q p ${\displaystyle \rightarrow }$ q T T T T F F F T T F F T
Biconditional (if and only if, xnor)	${\displaystyle \leftrightarrow }$, ${\displaystyle \equiv }$, ${\displaystyle =}$		p q p ${\displaystyle \leftrightarrow }$ q T T T T F F F T F F F T

Simplifying logical expressions

R-diagrams can be used to easily simplify complicated logical expressions, using a step-by-step process. Using order of operations, logical operators are applied to R-diagrams in the proper sequence. Finally, the result is an R-diagram that can be converted back into a simpler logical expression.

For example, take the following expression:

${\displaystyle (Q\leftrightarrow P)\lor (\lnot P\land Q)\,}$

It can be simplified using R-diagrams as follows:

${\displaystyle (}$ ${\displaystyle \leftrightarrow }$ ${\displaystyle )\lor (}$ ${\displaystyle \land }$ ${\displaystyle )}$

${\displaystyle \lor }$

which is equal to:

${\displaystyle P\rightarrow Q.\,}$

Proving logical arguments

Similarly, R-diagrams can be used to prove or disprove logical arguments. Take, for instance, the well known argument modus ponens, also known as implication elimination:

${\displaystyle {\frac {P\to Q,P}{\therefore Q}}}$

This can be converted into a tautological logical expression,

${\displaystyle ((P\to Q)\land P)\to Q}$

which can then be simplified using R-diagrams:

${\displaystyle ((}$ ${\displaystyle \to }$ ${\displaystyle )\land }$ ${\displaystyle )\to }$

${\displaystyle (}$ ${\displaystyle \land }$ ${\displaystyle )\to }$

${\displaystyle \to }$

The result is an R-diagram in which every space has a dot. This means the argument is a tautology; it is true in all cases. An R-diagram in which no space has a dot is a contradiction, a statement that is never true.

Application to set theory

See also: Set theory

R-diagrams are also used in set theory, as an alternative to Venn diagrams. In set theory, each line represents a set instead of a logical statement; A replaces p and B replaces q. When used for sets, a dot above the line represents inclusion, where a dot below represents exclusion. As in logic, basic set operations can be represented visually using R-diagrams:

Basic Set Operations

Name	Notation	R-Diagram
Union	${\displaystyle A\cup B}$
Intersection	${\displaystyle A\cap B}$
Absolute Complement	${\displaystyle A^{c}}$
Relative Complement (set difference)	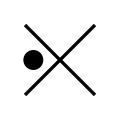${\displaystyle A\smallsetminus B}$
Symmetric Difference	${\displaystyle A\Delta B}$

R-diagrams illustrate the equivalence between the set theoretical and logical concepts: intersection in set theory is equivalent to conjunction in logic, and set theory's union is equivalent to the logical disjunction.

References

1. Barksdale, Jr., James B. (October 1970). "Sets and Randolph Diagrams" (PDF). Paper presented at the Louisville Regional Convention of the National Council of Teachers of Mathematics. Louisville, Kentucky: Western Kentucky University . Retrieved 2012-03-15.
2. Randolph, John F. (February 1965). "Cross-Examining Propositional Calculus and Set Operations". The American Mathematical Monthly. 72 (2). Mathematical Association of America: 117–127. doi:10.1080/00029890.1965.11970498. JSTOR   2310972.