
Geodesy is the Earth science of accurately measuring and understanding Earth's figure, orientation in space, and gravity. The field also incorporates studies of how these properties change over time and equivalent measurements for other planets. Geodynamical phenomena, including crustal motion, tides and polar motion, can be studied by designing global and national control networks, applying space geodesy and terrestrial geodetic techniques and relying on datums and coordinate systems. The job title is geodesist or geodetic surveyor.

In geography, latitude is a geographic coordinate that specifies the north–south position of a point on the Earth's surface. Latitude is an angle which ranges from 0° at the Equator to 90° at the poles. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude is used together with longitude to specify the precise location of features on the surface of the Earth. On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes that are used in special applications.

The geographic coordinate system (GCS) is a spherical or ellipsoidal coordinate system for measuring and communicating positions directly on the Earth as latitude and longitude. It is the simplest, oldest and most widely used of the various of spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.
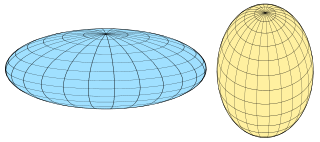
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).

The World Geodetic System (WGS) is a standard for use in cartography, geodesy, and satellite navigation including GPS. This standard includes the definition of the coordinate system's fundamental and derived constants, the normal gravity Earth Gravitational Model (EGM), a description of the associated World Magnetic Model (WMM), and a current list of local datum transformations.

Figure of the Earth is a term of art in geodesy that refers to the size and shape used to model Earth. The size and shape it refers to depend on context, including the precision needed for the model. The sphere is an approximation of the figure of the Earth that is satisfactory for many purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.
In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.

The Geodetic Reference System 1980 is a geodetic reference system consisting of a global reference ellipsoid and a normal gravity model.

A geodetic datum or geodetic system is a global datum reference or reference frame for precisely representing the position of locations on Earth or other planetary bodies by means of geodetic coordinates. are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a location across the Earth's surface, in latitude and longitude or another coordinate system; a vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). Since the rise of the global positioning system (GPS), the ellipsoid and datum WGS 84 it uses has supplanted most others in many applications. The WGS 84 is intended for global use, unlike most earlier datums.
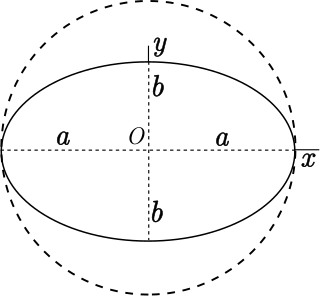
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is f and its definition in terms of the semi-axes of the resulting ellipse or ellipsoid is

A spatial reference system (SRS) or coordinate reference system (CRS) is a framework used to precisely measure locations on the surface of the Earth as coordinates. It is thus the application of the abstract mathematics of coordinate systems and analytic geometry to geographic space. A particular SRS specification comprises a choice of Earth ellipsoid, horizontal datum, map projection, origin point, and unit of measure. Thousands of coordinate systems have been specified for use around the world or in specific regions and for various purposes, necessitating transformations between different SRS.

The North American Datum (NAD) is the horizontal datum now used to define the geodetic network in North America. A datum is a formal description of the shape of the Earth along with an "anchor" point for the coordinate system. In surveying, cartography, and land-use planning, two North American Datums are in use for making lateral or "horizontal" measurements: the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). Both are geodetic reference systems based on slightly different assumptions and measurements.

The Earth-centered, Earth-fixed coordinate system, also known as the Geocentric coordinate system, is a cartesian spatial reference system that represents locations in the vicinity of the Earth as X, Y, and Z measurements from its center of mass. Its most common use is in tracking the orbits of satellites and in satellite navigation systems for measuring locations on the surface of the Earth, but it is also used in applications such as tracking crustal motion.
In geodesy and navigation, a meridian arc is the curve between two points on the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length.

An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.
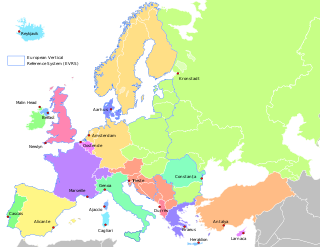
In geodesy, surveying, hydrography and navigation, vertical datum or altimetric datum, is a reference surface for vertical positions, such as the elevations of Earth-bound features and altitudes of satellite orbits and in aviation. In planetary science, vertical datums are also known as zero-elevation surface or zero-level reference.

Geodetic coordinates are a type of curvilinear orthogonal coordinate system used in geodesy based on a reference ellipsoid. They include geodetic latitude (north/south) ϕ, longitude (east/west) λ, and ellipsoidal heighth. The triad is also known as Earth ellipsoidal coordinates.
A planetary coordinate system is a generalization of the geographic coordinate system and the geocentric coordinate system for planets other than Earth. Similar coordinate systems are defined for other solid celestial bodies, such as in the selenographic coordinates for the Moon. The coordinate systems for almost all of the solid bodies in the Solar System were established by Merton E. Davies of the Rand Corporation, including Mercury, Venus, Mars, the four Galilean moons of Jupiter, and Triton, the largest moon of Neptune.














