
Angular momentum is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, flying discs, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as or where is the Laplace operator, is the divergence operator, is the gradient operator, and is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relative to a rotational axis. It is the ratio between the torque applied and the resulting angular acceleration about that axis. It plays the same role in rotational motion as mass does in linear motion. A body's moment of inertia about a particular axis depends both on the mass and its distribution relative to the axis, increasing with mass & distance from the axis.
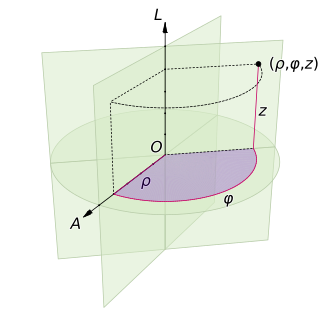
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.
A moment is a mathematical expression involving the product of a distance and a physical quantity such as a force or electric charge. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions; a list of examples is provided later.

In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude of torque the object experiences in a given magnetic field. When the same magnetic field is applied, objects with larger magnetic moments experience larger torques. The strength of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. Its direction points from the south pole to north pole of the magnet.
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress of a column.

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an or with a . In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system.
In geometry, the area enclosed by a circle of radius r is πr2. Here, the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko–Ehrenfest beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern created by waves passing through an aperture or around an object, when viewed from relatively close to the object. In contrast the diffraction pattern in the far field region is given by the Fraunhofer diffraction equation.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z).

In the field of solid mechanics, torsion is the twisting of an object due to an applied torque. Torsion could be defined as strain or angular deformation, and is measured by the angle a chosen section is rotated from its equilibrium position. The resulting stress is expressed in either the pascal (Pa), an SI unit for newtons per square metre, or in pounds per square inch (psi) while torque is expressed in newton metres (N·m) or foot-pound force (ft·lbf). In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius.
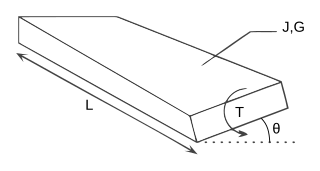
The torsion constant or torsion coefficient is a geometrical property of a bar's cross-section. It is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional stiffness. The SI unit for torsion constant is m4.

Rotational diffusion is the rotational movement which acts upon any object such as particles, molecules, atoms when present in a fluid, by random changes in their orientations. Although the directions and intensities of these changes are statistically random, they do not arise randomly and are instead the result of interactions between particles. One example occurs in colloids, where relatively large insoluble particles are suspended in a greater amount of fluid. The changes in orientation occur from collisions between the particle and the many molecules forming the fluid surrounding the particle, which each transfer kinetic energy to the particle, and as such can be considered random due to the varied speeds and amounts of fluid molecules incident on each individual particle at any given time.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.


























































