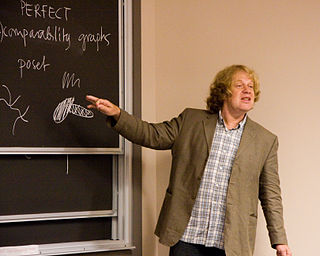In graph drawing and geometric graph theory, the slope number of a graph is the minimum possible number of distinct slopes of edges in a drawing of the graph in which vertices are represented as points in the Euclidean plane and edges are represented as line segments that do not pass through any non-incident vertex.
Although closely related problems in discrete geometry had been studied earlier, e.g. by Scott (1970) and Jamison (1984), the problem of determining the slope number of a graph was introduced by Wade & Chu (1994), who showed that the slope number of an n-vertex complete graph Kn is exactly n. A drawing with this slope number may be formed by placing the vertices of the graph on a regular polygon.
The slope number of a graph of maximum degree d is clearly at least , because at most two of the incident edges at a degree-d vertex can share a slope. More precisely, the slope number is at least equal to the linear arboricity of the graph, since the edges of a single slope must form a linear forest, and the linear arboricity in turn is at least .
Do the graphs of maximum degree four have bounded slope number?
There exist graphs with maximum degree five that have arbitrarily large slope number. [1] However, every graph of maximum degree three has slope number at most four; [2] the result of Wade & Chu (1994) for the complete graph K4 shows that this is tight. Not every set of four slopes is suitable for drawing all degree-3 graphs: a set of slopes is suitable for this purpose if and only if it forms the slopes of the sides and diagonals of a parallelogram. In particular, any degree 3 graph can be drawn so that its edges are either axis-parallel or parallel to the main diagonals of the integer lattice. [3] It is not known whether graphs of maximum degree four have bounded or unbounded slope number. [4]
As Keszegh, Pach & Pálvölgyi (2011) showed, every planar graph has a planar straight-line drawing in which the number of distinct slopes is a function of the degree of the graph. Their proof follows a construction of Malitz & Papakostas (1994) for bounding the angular resolution of planar graphs as a function of degree, by completing the graph to a maximal planar graph without increasing its degree by more than a constant factor, and applying the circle packing theorem to represent this augmented graph as a collection of tangent circles. If the degree of the initial graph is bounded, the ratio between the radii of adjacent circles in the packing will also be bounded by the ring lemma, [5] which in turn implies that using a quadtree to place each graph vertex on a point within its circle will produce slopes that are ratios of small integers. The number of distinct slopes produced by this construction is exponential in the degree of the graph.
It is NP-complete to determine whether a graph has slope number two. [6] From this, it follows that it is NP-hard to determine the slope number of an arbitrary graph, or to approximate it with an approximation ratio better than 3/2.
It is also NP-complete to determine whether a planar graph has a planar drawing with slope number two, [7] and hard for the existential theory of the reals to determine the minimum slope number of a planar drawing. [8]
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.
In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
A thrackle is an embedding of a graph in the plane in which each edge is a Jordan arc and every pair of edges meet exactly once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, they must cross at their intersection point: the intersection must be transverse.
The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:
In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
János Pach is a mathematician and computer scientist working in the fields of combinatorics and discrete and computational geometry.
In graph drawing, the angular resolution of a drawing of a graph is the sharpest angle formed by any two edges that meet at a common vertex of the drawing.
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.
In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.
In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.
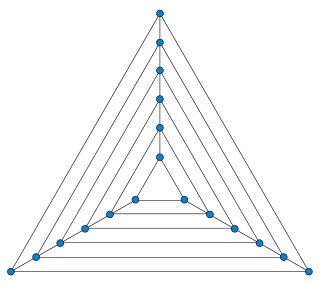
In graph theory, a nested triangles graph with n vertices is a planar graph formed from a sequence of n/3 triangles, by connecting pairs of corresponding vertices on consecutive triangles in the sequence. It can also be formed geometrically, by gluing together n/3 − 1 triangular prisms on their triangular faces. This graph, and graphs closely related to it, have been frequently used in graph drawing to prove lower bounds on the area requirements of various styles of drawings.
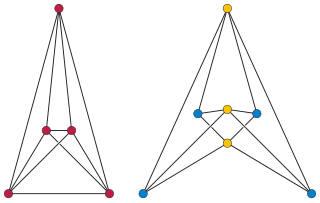
In graph drawing, a RAC drawing of a graph is a drawing in which the vertices are represented as points, the edges are represented as straight line segments or polylines, at most two edges cross at any point, and when two edges cross they do so at right angles to each other. In the name of this drawing style, "RAC" stands for "right angle crossing".
In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.
In graph drawing styles that represent the edges of a graph by polylines, it is desirable to minimize the number of bends per edge or the total number of bends in a drawing. Bend minimization is the algorithmic problem of finding a drawing that minimizes these quantities.
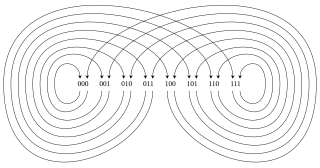
In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings.
In graph theory, a family of graphs is said to have bounded expansion if all of its shallow minors are sparse graphs. Many natural families of sparse graphs have bounded expansion. A closely related but stronger property, polynomial expansion, is equivalent to the existence of separator theorems for these families. Families with these properties have efficient algorithms for problems including the subgraph isomorphism problem and model checking for the first order theory of graphs.
In geometric graph theory, a penny graph is a contact graph of unit circles. It is formed from a collection of unit circles that do not cross each other, by creating a vertex for each circle and an edge for every pair of tangent circles. The circles can be represented physically by pennies, arranged without overlapping on a flat surface, with a vertex for each penny and an edge for each two pennies that touch.
In the geometry of circle packings in the Euclidean plane, the ring lemma gives a lower bound on the sizes of adjacent circles in a circle packing.
Conflict-free coloring is a generalization of the notion of graph coloring to hypergraphs.
